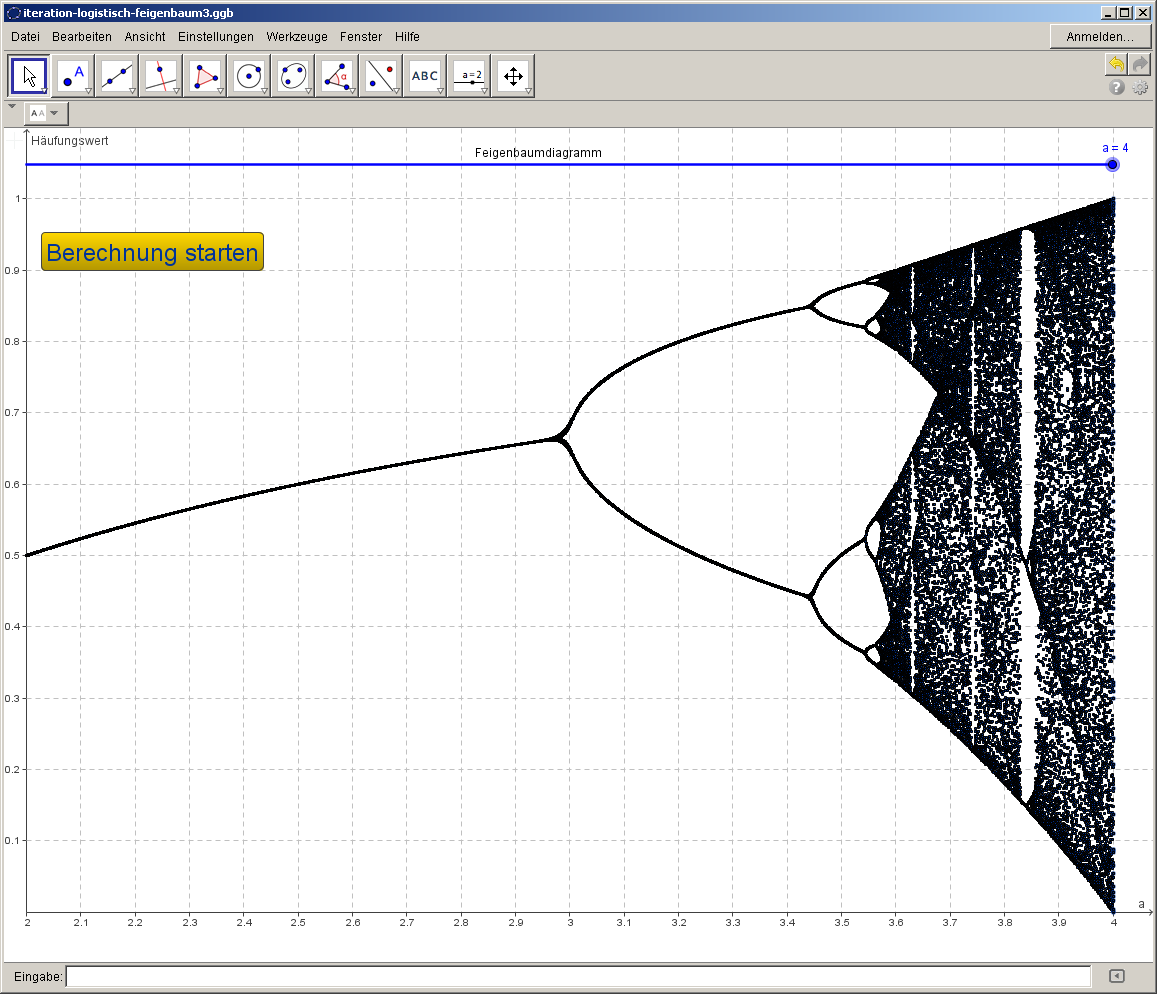
Feigenbaumdiagramm
Das logistische Wachstumsmodell beschreibt das Wachstum einer Population indem es das exponentielle Modell und das beschränkte Modell kombiniert. In diesem Artikel behandeln wir das Langzeitverhalten des logistischen Modells.
Im folgenden GeoGebra-Beispiel werden die Häufungspunkte bei der Rekursion in Abhängigkeit vom Parameter
dargestellt. Bis
erhalten wir einen Häufungswert, dann 2, 4, 8, … Häufungswerte. Es ist bezeichnend, dass die Häufungswerte mit zunehmendem
jeweils verdoppelt werden („Bifurkation“):
Aufgaben:
- Vergleiche mit dem logistischen Wachstumsmodell!
- Vergleiche mit dem diskreten logistischen Modell!
- Vergleiche mit dem Spinnwebdiagramm!
- Das Feigenbaumdiagramm ist selbstähnlich. Untersuche dies an Hand der „Gabelungen“!
Zurück zu Fraktale