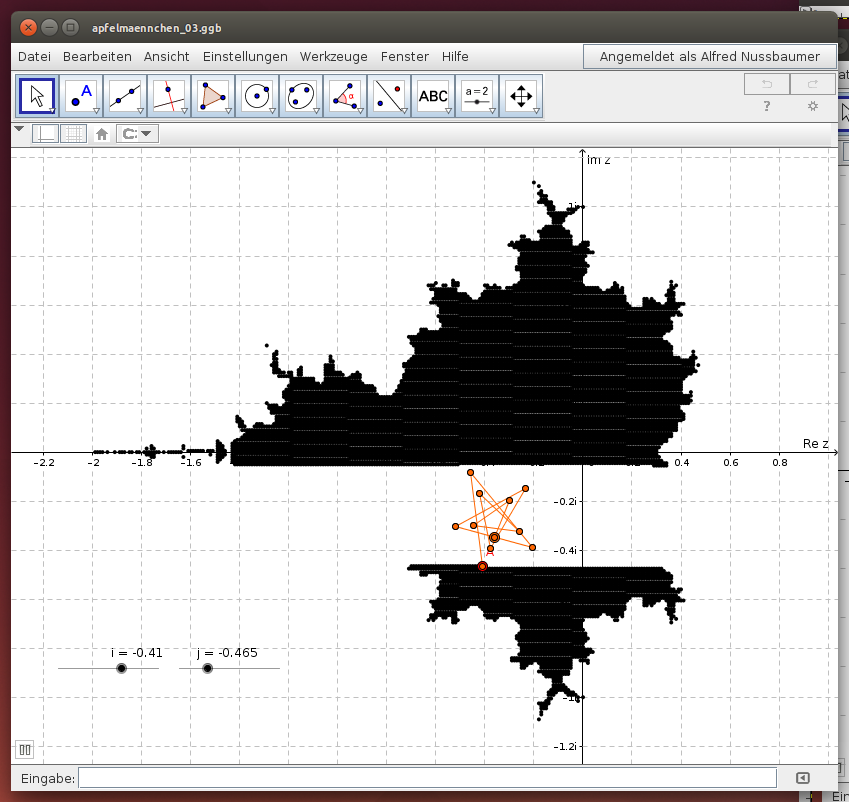
Die Mandelbrotmenge mit GeoGebra erzeugen
Die Mandelbrotmenge enthält alle komplexen Zahlen c, für die die Iteration , mit Startwert
gegen Null konvergiert. Im folgenden GeoGebra-Beispiel wird diese Menge Punkt für Punkt erzeugt, indem die Eigenschaften der Punkte in einem Rechteck in der Nähe von (0,0) der komplexen Zahlenebene untersucht werden. Stelle die beiden Schieberegler für i und j auf den Anfangswert i = -2, j=-1.1 und starte die Animation:
Aufgaben:
- Beschreibe, unter welchen Bedingungen eine komplexe Zahl zur Mandelbrotmenge gehört!
- Für Unentwegte: Entwickle auf der Basis des obigen GeoGebra-Beispiels ein GeoGebra-Beispiel, mit dem kleine Bereiche der Mandelbrotmenge untersucht werden können!
- Untersuche den Zusammenhang zwischen der Mandelbrotmenge und der Juliamenge!
Zurück zu Lernpfad Fraktale