Fortlaufende Potenzen komplexer Zahlen
Wir beobachten die Zahlenfolge z, z2, z3, z4, …, woebei der Betrag der Zahl z kleiner, gleich oder größer als 1 sein kann.
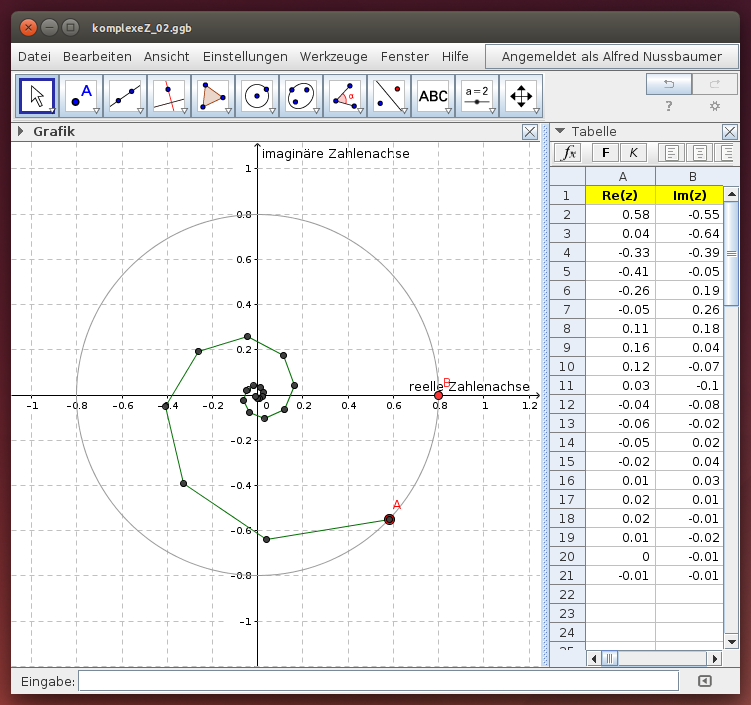
Wähle im folgenden GeoGebra-Beispiel den Betrag der komplexen Zahl z mit dem roten Punkt B auf der reellen Zahlenachse und anschließend die Zahl z, indem du den roten Punkt A auf dem Mittelpunktskreis verschiebst:
Aufgaben:
- Gib an, unter welchen Bedingungen die Folge z, z2, z3, z4, … konvergiert! Hängt dies von der Lage der Zahl z auf dem Mittelpunktskreis ab?
- Gib an, unter welchen Bedingungen die Folge z, z2, z3, z4, … divergiert! Hängt dies von der Lage der Zahl z auf dem Mittelpunktskreis ab?
- Vergleiche mit der Iteration zur Mandelbrotmenge!
Zurück zu Lernpfad Komplexe Zahlen | Komplexe Zahlen und algebraische Gleichungen | Fraktale