Selbstähnliche Figuren mit GeoGebra konstruieren
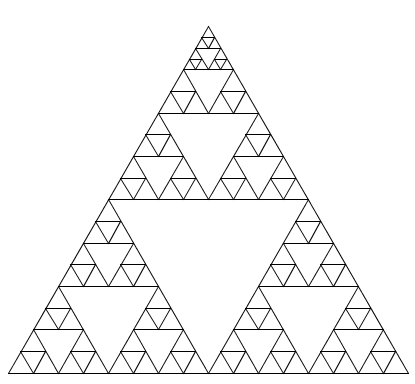
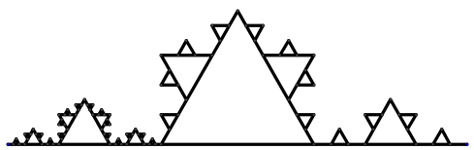
Zu den bekanntesten fraktalen Objekten gehören das Sierpinski-Dreieck und die Kochkurve. Sie lassen sich mit GeoGebra in einigen Schritten rasch konstruieren.
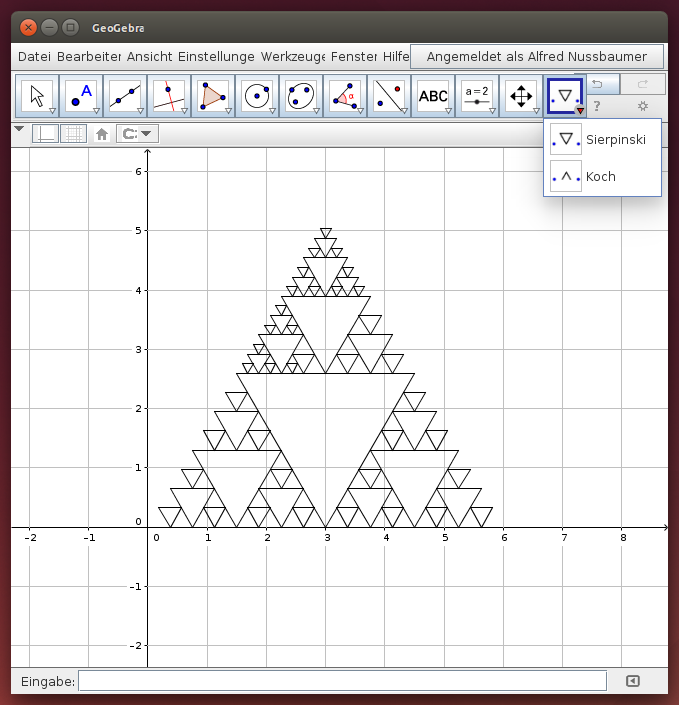
Im folgenden GeoGebra-Beispiel können ähnliche Figuren mit GeoGebra-Werkzeugen rasch konstruiert werden. Wähle eine Ausgangsstrecke mit zwei Endpunkten und wende darauf das gewünschte Werkzeug an. Das GeoGebra-Beispiel stellt das Werkzeug Sierpinski zur Konstruktion des Sierpinski-Dreiecks und das Werkzeug Koch zur Konstruktion der Kochkurve zur Verfügung:
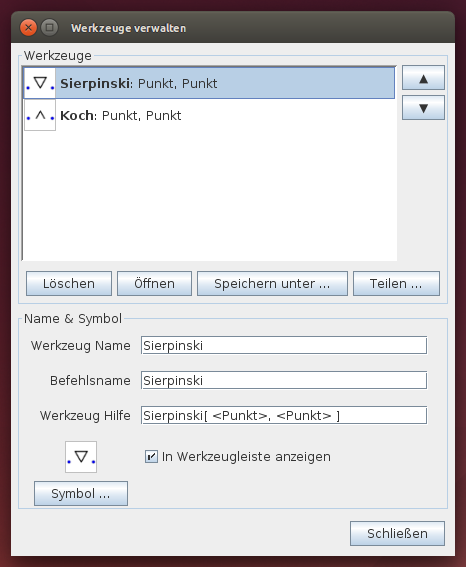
Hinweis: Mit dem Befehl „Werkzeuge verwalten“ können die beiden Werkzeuge „Sierpinski“ und „Koch“ in der Werkzeugleiste angezeigt werden.
Aufgaben:
- Ziehe die Ausgangsstrecke größer und untersuche die Selbstähnlichkeit des konstruierten Fraktals!
- Entwirf geeignete Werkzeuge für weitere Fraktale (Sierpinski-Teppich, Cantor-Staub, …)
Zurück zu Lernpfad Fraktale