Trichter mit maximalem Volumen
Ein Trichter hat die Gestalt einer auf dem Kopf stehenden quadratischen Pyramide (ohne Basisfläche). Wie ist er bei einer gegebenen Oberfläche zu dimensionieren, damit sein Volumen maximal wird?
Die Oberfläche des Trichters ist im Beispiel O = 1 E2, die Höhe h des Prismas hängt somit von der Wahl der Basiskante a ab.
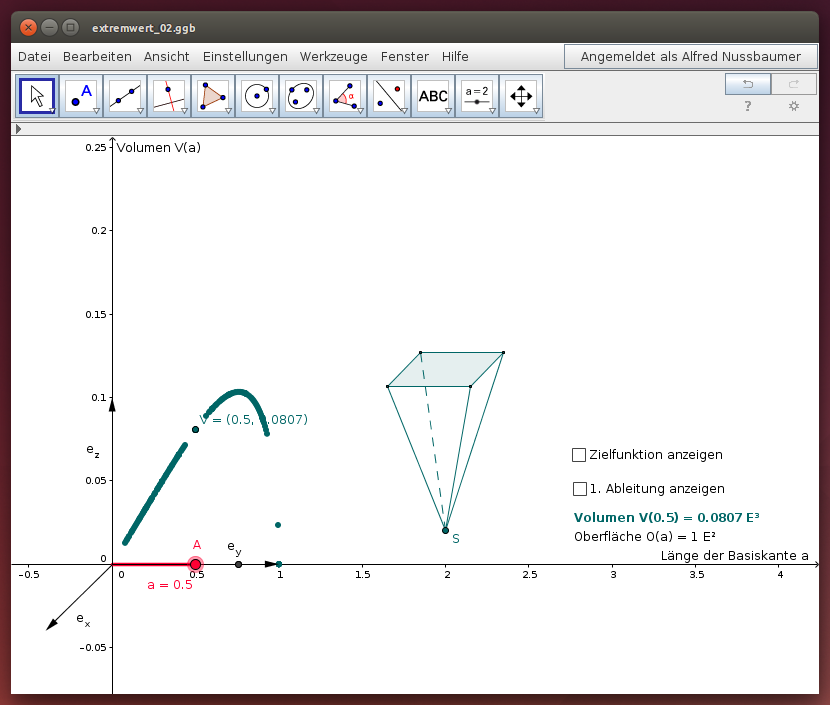
Wähle die Länge der Basiskante a zwischen 0 und 1 E, indem du im folgenden GeoGebra-Applet den roten Punkt A verschiebst. Die entsprechende Form des Trichters wird im Schrägriss angezeigt. Die vertikale Koordinate des Punktes V stellt den jeweiligen Rauminhalt des Trichters abhängig von der Länge der Basiskante a dar:
Aufgaben:
- Bei welchen Abmessungen ist das Volumen des Trichters maximal? Kontrolliere dein Ergebnis mit Hilfe der Zielfunktion und mit ihrer 1. Ableitung!
- Bei welchen Abmessungen ist das Volumen minimal? Diskutiere die zugehörigen Abmessungen und die Form des Trichters!
- Löse die Aufgabe mit Hilfe einer Tabelle!
- Berechne die Zielfunktion, die erste Ableitung und die Extremstelle!
Zurück zu Anwendungen der Differentialrechnung | Extremwertaufgaben | Räumliche Aufgaben | Thema Polynomfunktionen