Temperaturausgleich
Um von einem diskreten Modell zu einem kontinuierlichen Modell zu gelangen, wird die Differenzengleichung mittels Grenzwert für in eine Differenzialgleichung umgewandelt.
Beispiel: Abkühlkurve (beschränktes Wachstum)
80°C heißes Wasser kühlt bei einer Raumtemperatur von 20°C während eines Zeitraumes von 60 Minuten ab. Bestimme die Abkühlkurve!
Differenzengleichung:
mit
Differentialgleichung:
mit
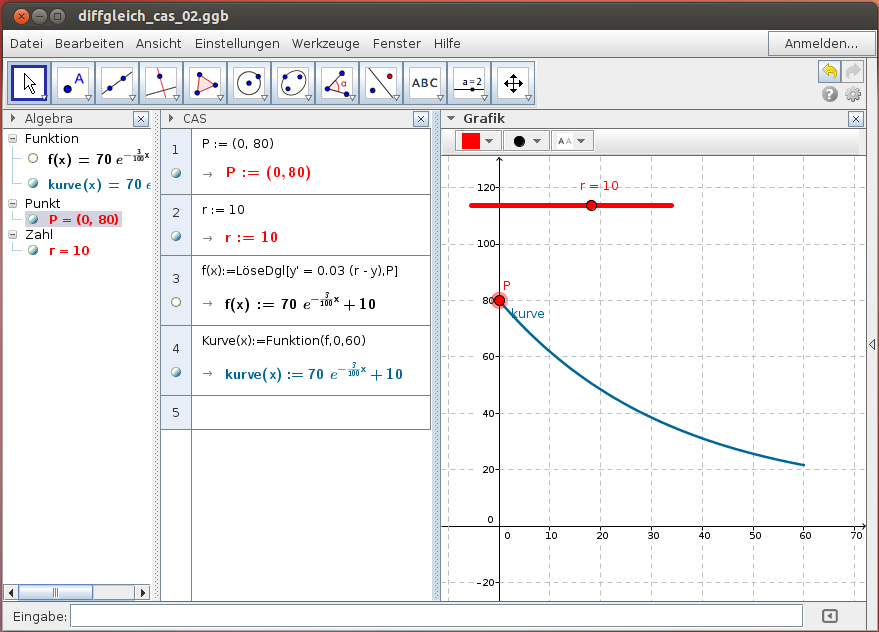
Wir lösen die Differentialgleichung exakt in der CAS-Ansicht:
- Lege die Anfangsbedingungen (z.B. Punkt P auf der Kurve, Raumtemperatur, …) fest.
- Der CAS-Befehl
LöseDgl(<y'=f(x,y)>, P)versucht, eine exakte Lösung zu bestimmen. - Stelle einen sinnvollen Bereich mit dem Befehl
Funktion(<Funktion>,<Bereich>)dar.
Aufgaben:
- Vergleiche mit dem diskreten Modell zum Temperaturausgleich!
- Untersuche, wie die Lösung vom Ausgangswert P (Ausgangstemperatur) und von der Raumtemperatur r abhängt!
- Vergleiche mit der numerischen Lösung in der Algebra-Ansicht (Temperaturausgleich)!
Zurück zu Dynamische Systeme