Extremwertaufgabe - Abstandsberechnung 2
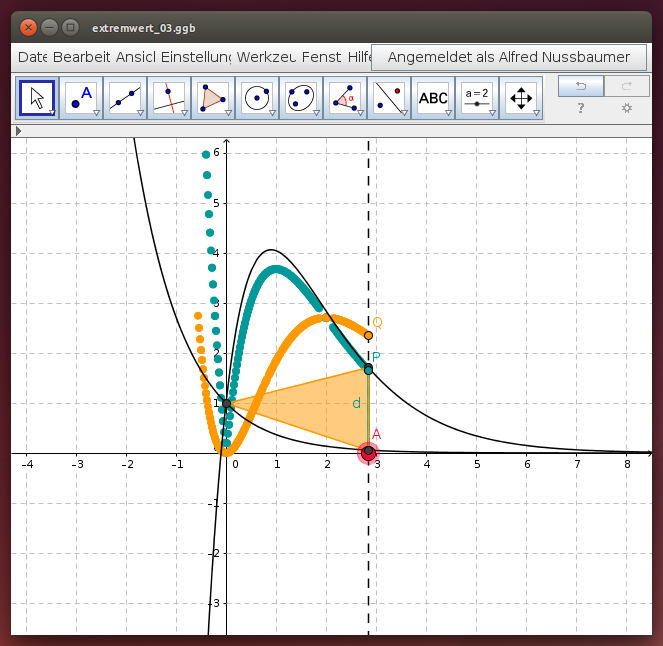
a) Lege eine senkrechte Gerade und bestimme ihre Schnittpunkte mit den beiden Kurven. Der Abstand d dieser beiden Schnittpunkte variiert - wo ist dieser Abstand am größten?
b) Verbinde die Schnittpunkte der senkrechten Geraden mit den beiden Funktionsgraphen mit ihrem gemeinsamen Punkt auf der y-Achse: Du erhältst ein Dreieck. Bei welcher Lage des Punktes A ist der Flächeninhalt des Dreiecks am größten?
Verschiebe den Punkt A auf der x-Achse und beobachte den Abstand d der beiden Schnittpunkte und den Flächeninhalt des Dreiecks!
Der Abstand erscheint als Punktespur P.
Der Flächeninhalt des Dreiecks erscheint als Punktespur Q.
Aufgaben:
- Gib eine Formel für den Abstand d an!
- Gib eine Formel für den Flächeninhalt des Dreiecks an!
- Löse die beiden Aufgaben mit Hilfe geeigneter Tabellen!
- Löse die beiden Extremwertsaufgaben mit Hilfe geeigneter **Zielfunktionen*!
- Öffne das GeoGebra-Applet und variiere die zweite Funktion g(x) = (a x + 1) exp(-x). Wie wirkt sich die Variation des Parameters a auf die Lösungen der beiden Extremwertsaufgaben aus?
Zurück zu Anwendungen der Differentialrechnung | Extremwertaufgaben | Ebene Aufgaben | Thema Polynomfunktionen