Inhaltsverzeichnis
Lernpfad: Das bestimmte Integral
8, S. 6 - 36, S. 46 - 70
Wir untersuchen einen zentralen Begriff der Differential- und Integralrechnung, das Integral. Hier lernen wir zunächst die Bedeutung des bestimmten Integrals als Flächeninhalt unter einer Kurve in einem zweidimensionalen Koordinatensystem kennen. Zunächst berechnen wir den Inhalt einer geradlinig begrenzten Fläche. Dies ist bei einer konstanten, homogenen linearen oder inhomogenen linearen Funktion der Fall.
Der Flächeninhalt unter einer Kurve
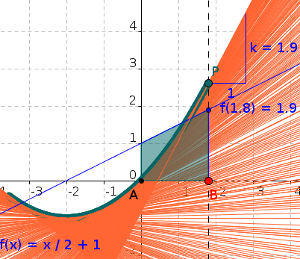
Bei allen anderen Funktionen können wir den Flächeninhalt im Allgemeinen nicht mit den bekannten Flächenformeln aus der Geometrie berechnen. Hier verwenden wir zunächst eine näherungsweise Berechnung:
Die Stammfunktion
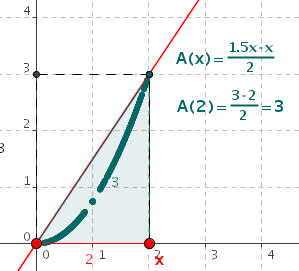
Interpretiere die Stammfunktion A(x) zu einer gegebenen Funktion f(x) als Flächeninhalt unter der Funktion im Intervall [0; x]!
Es gilt …
A(x) ist Stammfunktion von f(x), wenn gilt: A'(x) = f(x)
Es sei F(x) eine Stammfunktion von f(x). Untersuche die Ableitung F'(x) …
Lassen sich Stammfunktionen einfach berechnen? In manchen Fällen schon … beachte dabei, dass gilt:
Es gilt …
,
(
k … konstanter Faktor)
Ein konstanter Faktor bleibt beim Bilden der Stammfunktion unverändert.
,
,
Summenregel: Die Stammfunktion einer Summe von Funktionen ist einfach die Summe der einzelnen Stammfunktionen.
Weiter zu Stammfunktionen berechnen (Zuordnungsübungen)
Der Flächeninhalt als bestimmtes Integral
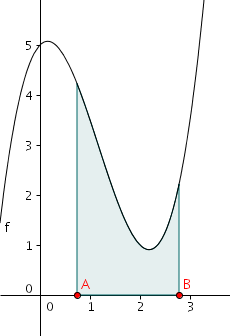Die Berechnung eines Flächeninhalts unter einer Kurve ist mit dem bestimmten Integral möglich:
ist der Inhalt der Fläche unter der Kurve f(x) im Intervall [a; b].
Dieses bestimmte Integral wird mit Hilfe der Stammfunktion F(x) (F'(x) = f(x)) berechnet.
Es gilt …
Ist die Stammfunktion F(x) bekannt, so gilt: .
Überprüfe dies anhand der folgenden Beispiele:
Eigenschaften des bestimmten Integrals
Die Eigenschaften des bestimmten Integrals, die sich direkt aus der Flächenberechnung ablesen lassen, erweitern wir auf negative Ergebnisse:
Weiter zu Lernpfad Flächenberechnung
Stammfunktionen berechnen
Übe das Bestimmen von Stammfunktionen (Zuordnungsübungen):
Weitere Anwendung des bestimmten Integrals
Das bestimmte Integral eignet sich nicht nur für die Berechnung von Flächeninhalten:
Zurück zu Thema Mathematik - 8. Klasse
