Das bestimmte Integral: Flächeninhalt unter der inhomogenen linearen Funktion

(zu tm.jpg 8)

Wir untersuchen, wie der Flächeninhalt unter der inhomogenen linearen Funktion tex:f(x) = k \cdot x + d von der rechten Grenze x abhängt.

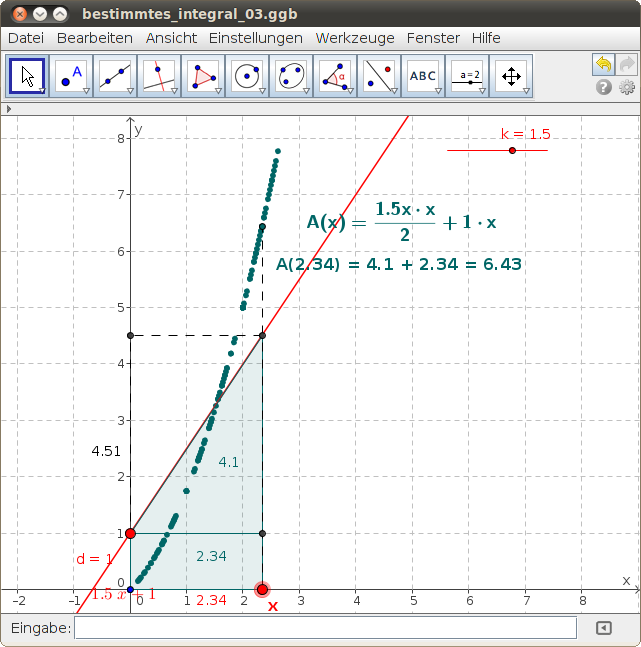
Wähle die rechte Grenze x für die Fläche indem du im folgenden GeoGebra-Beispiel den roten Punkt auf der x-Achse verschiebst und beobachte die Spur des Punktes, der den Flächeninhalt A(x) darstellt:

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Aufgaben:

  • Der rote Punkt auf der y-Achse legt die Konstante d fest. Wähle andere Werte für d, indem du ihn auf der y-Achse verschiebst! Lösche die Punktespur (STRG F) und beschreibe die neue Punktespur.
  • Wähle mit dem Schieberegler für k andere Werte, lösche die Punktespur (STRG F) und beschreibe die neue Punktespur.
  • Lies aus der Punktespur eine mögliche Funktionsgleichung für A(x) ab!
  • Rechne nach, dass für die Flächenfunktion tex:A(x) = \frac {k \cdot x^2} 2 + d x gilt!
  • Überprüfe und begründe, dass die Fläche unter der Kurve f durch Addition zweier Teilflächen bestimmt wird!

Zurück zu Thema Mathematik 8. Klasse | Das bestimmte Integral


Zuletzt angesehen: • bestimmtes_integral_03