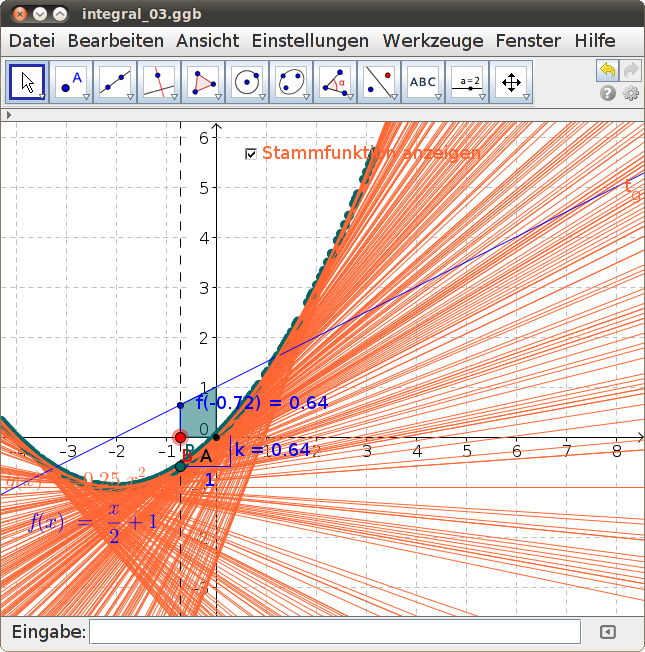
Die Ableitung der Stammfunktion
Die Stammfunktion g(x) zu einer gegebenen Funktion f(x) entspricht dem Flächeninhalt unter der Funktion f im Intervall [0; x]! Verschiebe dazu im folgenden GeoGebra-Beispiel die rechte Intervallgrenze mit dem roten Punkt B und erzeuge damit die Spur des Punktes P. Gleichzeitig wird im Punkt P wird die Gerade gezeichnet, deren Steigung dem Funktionswert f an der selben Stelle entspricht. Beobachte die Einhüllende dieser Geraden!
Aufgaben:
- Überprüfe: Die Stammfunktion g(x) ist die Einhüllende der Geraden in P.
- Die Steigung jeder Tangente an die Stammfunktion an der Stelle x entspricht genau dem Funktionswert der Funktion f(x). Formuliere den Zusammenhang zwischen der Stammfunktion g(x) und der gegebenen Funktion f(x)!
- Wähle verschiedene Funktionen f(x) durch Eingabe der Funktionsgleichung in die Eingabezeile (Achte darauf, dass die Funktion für x = 0 definiert ist)!
Zurück zu Grundlagen der Integralrechnung