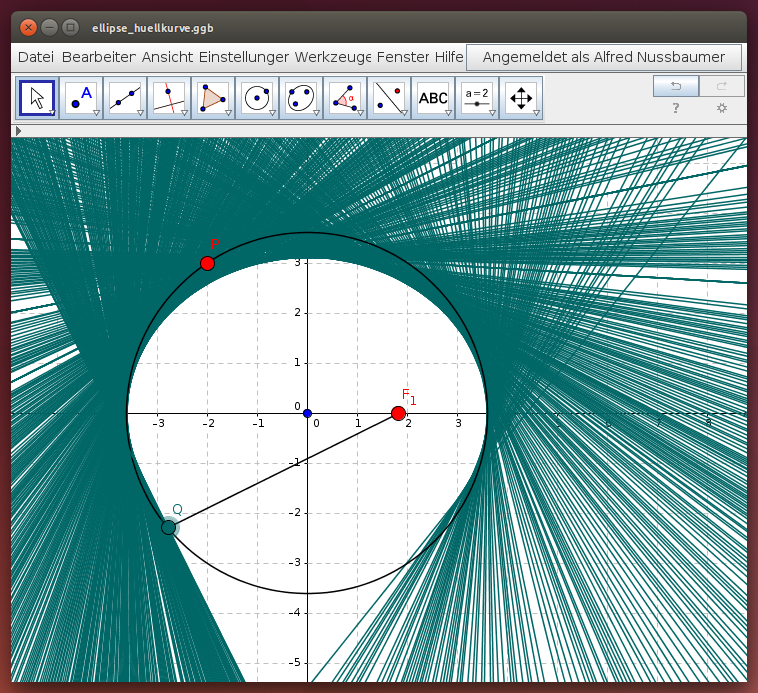
Die Hüllkurven - Definition für die Ellipse
Verschiebe im folgenden GeoGebra-Applet den roten Punkt P und lege damit den Radius des Mittelpunktskreises fest. Verschiebe nun den Punkt Q auf der Kreislinie und beobachte die Spur der Normalen auf die Strecke F1Q: Alle diese Geraden bilden eine Hüllkurve - welche Form hat diese?
Aufgaben:
- Verschiebe den Brennpunkt F1, ermittle die Hüllkurve und beschreibe, wie die Form der Ellipse von der Lage des Brennpunkts F1 in Bezug auf den gegebenen Kreis abhängt (Tipp: Mit <STRG>-F wird die Spur der Geraden gelöscht)!
- Schiebe den Brennpunkt F1 aus dem gegebenen Kreis heraus: Entsteht wieder eine Hüllkurve? Wenn ja: Beschreibe ihre Form!
Weiter zu Hüllkurvendefinition der Parabel | Hüllkurvendefinition der Hyperbel | Hüllkurve
Zurück zu Nichtlineare analytische Geometrie R2