Wann ist die Katakaustik eine Herzkurve?
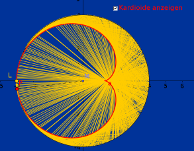
 Wir untersuchen die Katakaustik einer kreisförmigen Reflexionsfläche, wenn eine punktförmige Lichtquelle vorliegt. Im folgenden GeoGebra-Applet liegt die Lichtquelle L auf der Kreislinie; sie ist auch ein Punkt der Herzkurve (Kardioide).
Wir untersuchen die Katakaustik einer kreisförmigen Reflexionsfläche, wenn eine punktförmige Lichtquelle vorliegt. Im folgenden GeoGebra-Applet liegt die Lichtquelle L auf der Kreislinie; sie ist auch ein Punkt der Herzkurve (Kardioide).
Verschiebe im folgenden GeoGebra - Applet den roten Punkt entlang der Kreislinie und beobachte die Einhüllende der reflektierten Strahlen:
Online-Hilfe — Download — Erstellt mit © GeoGebra durch TM-Team
Tipp: Mit <Strg> - F wird der Bildschirm neu aufgebaut; die eingezeichnete Spur wird gelöscht.
Aufgaben:
- Die Herzkurve im obigen Applet hat die Formel a(t) = [8/3 cos(t) - 4/3 cos (2t), 8/3 sin (t) - 4/3 sin (2t)]. Prüfe nach!
- Wie müsste die Formel der Herzkurve für alle möglichen Kreisradien der spiegelnden Flächen lauten?
Weiter zu Katakaustik | Herzkurve | Parametrisierte Kurven | Hüllkurve | Brennpunkt