Funktionen
zu  5, S. 101- S. 150 5, S. 101- S. 150 | Technologie-Zugänge zu ausgewählten Aufgaben |
Aufgabe TM5-617
Die Polizei kann bei einer Notbremsung aufgrund der Länge des Bremsweges die Geschwindigkeit eines Autos feststellen. Bei trockener Fahrbahn gilt:
| Bremsweg | Geschwindigkeit |
| 20 m | 50 km/h |
| 40 m | 72 km/h |
| 60 m | 88 km/h |
| 80 m | 102 km/h |
| 100 m | 114 km/h |
| 120 m | 125 km/h |
| 140 m | 135 km/h |
Lege die unabhängige und die abhängige Variable fest. Zeichne den Funktionsgraphen und verbinde, falls dies sinnvoll ist, die einzelnen Punkte.
Ausführung mit GeoGebra
Hinweise:
Trage zuerst die Werte in der Tabellenansicht ein.
Markiere die Werte und erzeuge mit (rechter Maustaste)eine Liste von Punkten.
Diese Liste wird automatisch geplottet.
Willst du die Punkte geeignet verbinden, so verwende dazu den Befehl TrendLinie(Liste), hier besser noch TrendPot(Liste)
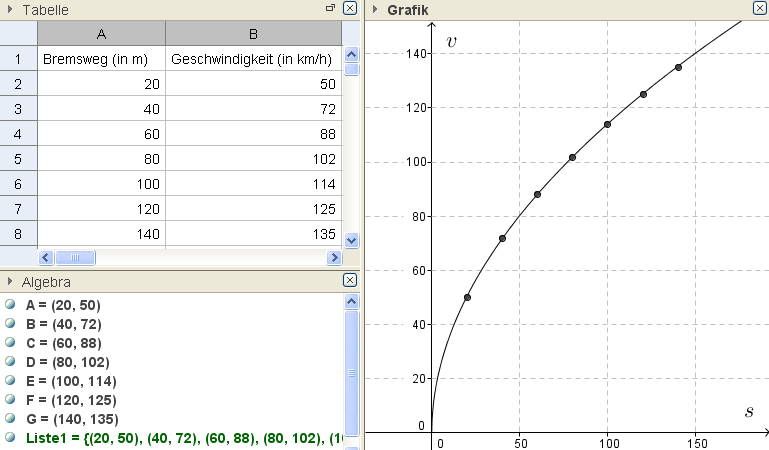
(zum Öffnen auf Abb. klicken)
Aufgabe TM5-644
Die Funktion ist durch ihren Term und die Definitionsmenge gegeben. Berechne für die ganzzahligen $x$-Werte die Funktionswerte.
a) $f(x) = \frac{5}{x + 4}\qquad \mathbb{D}_f = [−3;1]$
Ausführung mit GeoGebra
Hinweis:
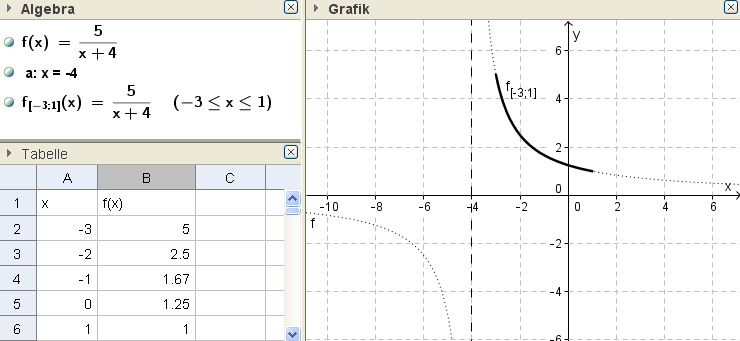
(zum Öffnen auf Abb. klicken)
b) $f(x) = |x| + 2\qquad \mathbb{D}_f = [−2;2]$
Ausführung mit GeoGebra
Hinweise:
Der Absolutbetrag wird mit der Funktion abs(x) angegeben.
Die gegebene Funktion lässt sich mit dem Befehl Wenn[-2 ≤ x ≤ 2, f] auf das Intervall [-2;2] einschränken.

(zum Öffnen auf Abb. klicken)
Aufgabe TM5-655
Aufgabe TM5-656
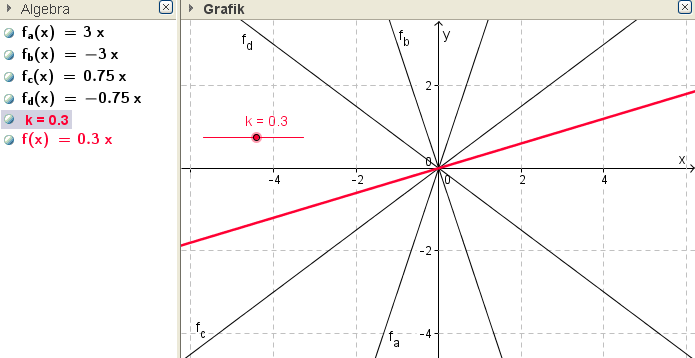
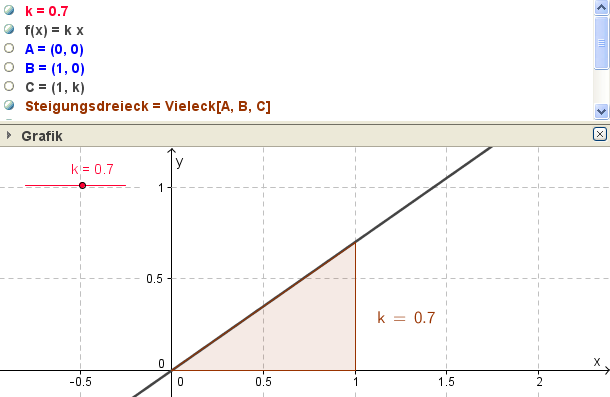
Zeichnet unterschiedliche homogene lineare Funktionen, indem ihr die Steigung $k$ variiert.
Notiert euch: Was haben alle Graphen gemeinsam? Worin unterscheiden sie sich?
Ausführung mit GeoGebra
Aufgabe TM5-667
Zeichnet die Funktionen der Aufgaben 661 − 663. Wählt einen günstigen Ausschnitt!
Ausführung mit GeoGebra
Hinweise:
Wenn du die Steigung $k$ und den Ordinatenabschnitt $d$ als eigene Werte eingibst, erhältst du durch Anklicken von $k$ und $d$ Schieberegler mit denen die Steigung und der Ordinatenabschnitt beliebig variiert werden kann.
Gehe für die Aufgaben 662 und 663 analog vor.
Mit dem Befehl Wenn[-3⇐x⇐3,f]] kannst du die Funktion auf ein vorgegebenes Definitionsintervall, hier z.B. auf $\mathbb{D}_f=[-2;2]$ einschränken.

(zum Öffnen auf Abb. klicken)
Siehe auch: Lineare Funktion
Aufgabe TM5-668
Zeichnet unterschiedliche inhomogene lineare Funktionen. Was haben alle Graphen gemeinsam? Worin unterscheiden sie sich?
Ausführung mit GeoGebra
Hinweis: Wenn du die Steigung $k$ und den Ordinatenabschnitt $d$ als eigene Werte eingibst, erhältst du durch Anklicken von $k$ und $d$ Schieberegler mit denen die Steigung und der Ordinatenabschnitt beliebig variiert werden kann.

(zum Öffnen auf Abb. klicken)
Siehe auch: Lineare Funktion
Aufgabe TM5-680
Überlegt einen Zusammenhang, der mit einem linearen Modell beschrieben werden könnte. Sucht nach entsprechenden Daten und stellt das Modell auf. Verwendet schließlich dieses Modell, um selbst formulierte Fragen zu beantworten.
Siehe Lineares Wachstum
Aufgabe TM5-727
Gebt quadratische Funktionen an, deren Scheitel die $x$-Koordinate $x_S = 3$ hat und die keine Nullstellen haben.
Ausführung mit Geogebra
Hinweise:
Geschickterweise gibst du die quadratische Funktion in der Scheiteldarstellung $f(x)=(x-x_S)^2+y_S$ an (vgl. Aufgabe TM5-723)
Wenn du die Koordinate $y_S$ anklickst, erhältst du einen Schieberegler mit dem du den Graphen der Parabel vertikal verschieben kannst

Du erkennst: wenn der Wert des konstanten Koeffizienten $c>9$ ist, ist die geforderte Bedingnung erfüllt.
Aufgabe TM5-728
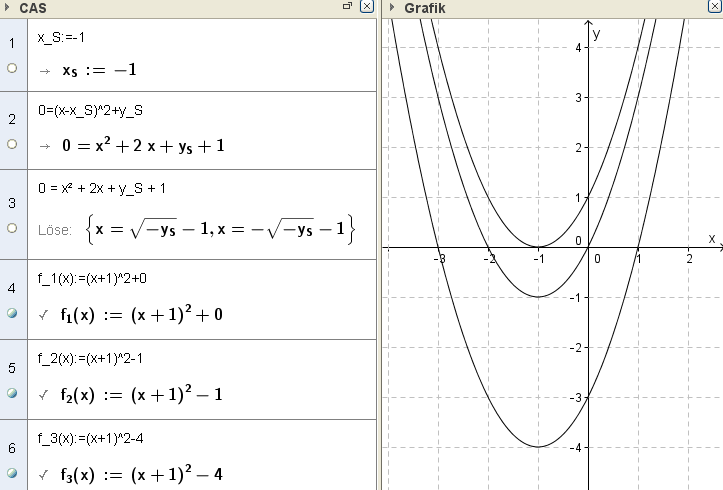
Gebt quadratische Funktionen an, deren Scheitel die $x$-Koordinate $x_S = −1$ hat und die ganzzahlige Nullstellen haben.
Ausführung mit GeoGebra
Hinweise:
Wir arbeiten mit der Scheiteldarstellung $f(x)=(x-x_S)^2+y_S$ an (vgl. Aufgabe TM5-723) und legen zuerst $x_S =-1$ fest.
Wir müssen nun die $y$-Koordinate des Scheitels $y_S$ so wählen, dass sich für die Nullstellen ganzzahlige Werte ergeben. Dazu lösen wir die Gleichung $f(x)=0$ bzw. $(x-x_S)^2+y_S=0$, diese ergibt die beiden Lösungen $x_{1,2}=1\pm \sqrt{-y_S}$
Ganzzahlige Werte für die Nullstellen erhalten wir also dann, wenn der Ausdruck unter der Wurzel eine Quadratzahl ist, also für $x=0,-1,-4,-9,-16,\dots$.
Aufgabe TM5-746
Ein Uhrenhersteller möchte den Preis für sein neues Modell festlegen und führt dazu eine Markt-
analyse durch. Das Ergebnis lautet: Bei einem Preis von 60 € ist der jährliche Gewinn 50 000 €,
bei einem Preis von 90 € ist der Gewinn 140 000 € und bei einem Preis von 130 € liegt der Gewinn
bei 120 000 €.
a) Ermittle ein quadratisches Modell für den Zusammenhang „Preis einer Uhr − Jahresgewinn“.
b) Zeichne die Funktion für Preise zwischen 30 € und 170 €.
c) Wie muss man den Preis einer Uhr festlegen, damit der Jahresgewinn maximal ist? Wie hoch
ist dieser Gewinn?
d) Gib an, wie der Preis der Uhr festgelegt werden darf, damit die Firma einen Gewinn macht.
Ausführung mit GeoGebra
Hinweise:
Für jede Information kannst du eine Gleichung anschreiben (Zeile #1-#3)
Markiere die drei Zeilen und verwende das Lösungswerkzeug (Icon “=“), du erhältst die Lösungen für die Koeffizienten a,b und c.
Nun kannst du die Funktion für den Gewinn in Abhängigkeit von Preis formulieren.
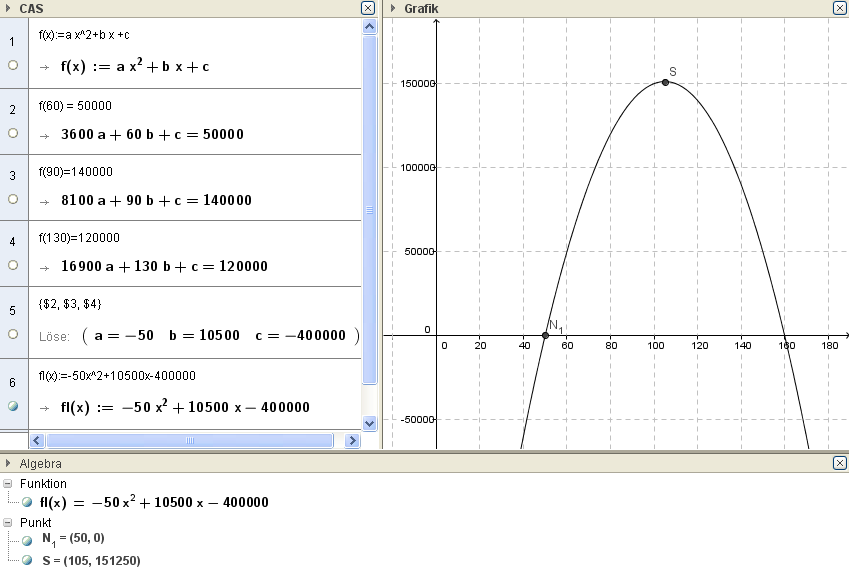
ad c) Der Jahresgewinn ist also bei einem Preis von 105€ maximal. Dieser Gewinn beträgt 151250€.
ad d) Die Firma erzielt einen Gewinn, wenn der Preis einer Uhr zwischen 50€ und 160€ liegt.
Aufgabe TM5-764
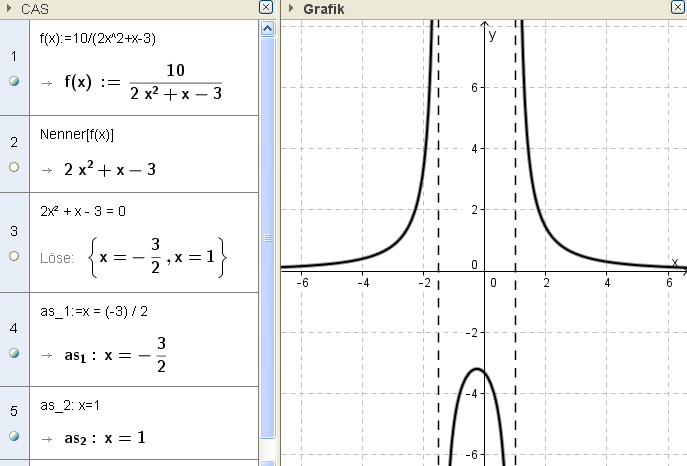
Die Funktion $f$ mit $f(x) =\frac{10}{2 x^2 + x − 3}$ hat zwei vertikale Asymptoten $as_1$ und $as_2$.
Findet heraus welche das sind und zeichnet den Funktionsgraphen.
Ausführung mit GeoGebra
Hinweise:
Vertikale Asyomptoten sind bei den Nullstellen des Nenners zu finden. Dort ist die Funktion nicht definiert und der Graph läuft in der Nähe „gegen Unendlich“.
Du kannst auf den Nenner enes Bruchterms mit dem Befehl Nenner(Term) zugreifen.
Aufgabe TM5-773
Eine U-Bahngarnitur fährt von einer Haltestelle zur nächsten. Die Funktion f beschreibt,
welche Strecke sie x Sekunden nach der Abfahrt zurückgelegt hat.

Zeichnet den Funktionsgraphen. Wie weit sind die beiden Stationen voneinander entfernt?
Wann beschleunigt bzw. wann bremst die U-Bahngarnitur? Wann fährt sie mit konstanter Geschwindigkeit? Skizziert den Graphen der Geschwindigkeitsfunktion.
Ausführung mit GeoGebra
Hinweise:
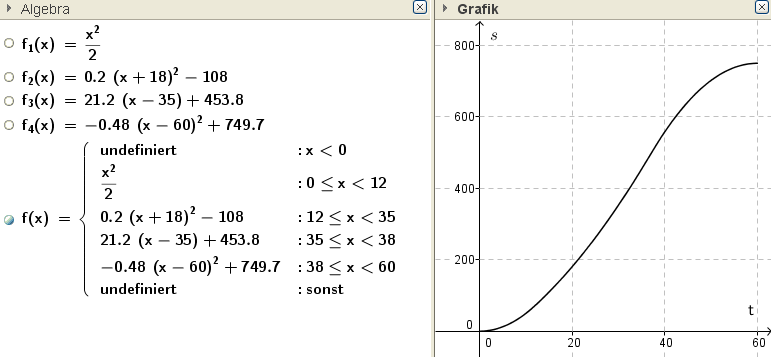
Gib zuerst die Teilfunktionen ein (Indizes kannst du mit einem Unterstrich angeben, z.B. f_1(x)= …)
Die abschnittsweise definierte Funktion gibst du am besten „aufsteigend“ in der Form
Wenn[x < 0, ?, Wenn[x < 12, f_1, Wenn[x < 35, f_2, Wenn[x < 38, f_3, Wenn[x < 60, f_4, ?]]]]]
einn. Achte dabei auf die korrekte Klammernsetzung.
Aufgabe TM5-787
Zwei Körper mit den Massen $m$ und $M$ ziehen einander mit der Kraft
$F=\frac{G\cdot m\cdot M}{r^2}$
an ($G$ … Gravitationskonstante, $r$ … Abstand).
Leitet aus dieser Formel sinnvolle Funktionen ab. Um welche Art von Funktion handelt es sich
jeweils?
Ausführung
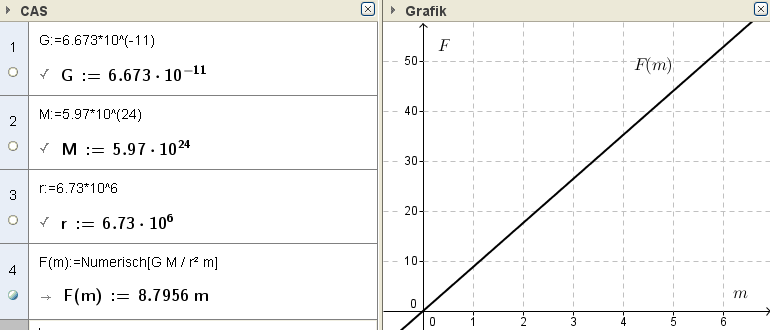
(1) Wir können z.B. die Anziehungskraft $F$ als Funktion der Masse $m$ auffassen, damit ergibt sich eine lineare Funktion $f(x)=k\cdot x$ (Funktion der direkten Proportionalität).
Wenn wir für $G$ die Gravitationskonstante einsetzen, für $M$ die Erdmasse und für $r$ den Erdradius, dann beschreibt diese Funktion beschreibt das Gewicht der Masse $m$.
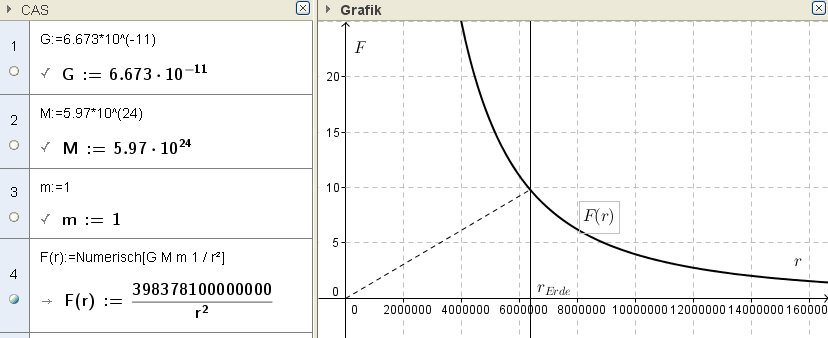
(2) Wir können z.B. die Anziehungskraft $F$ als Funktion des Radius $r$ auffassen, damit ergibt sich eine Funktion des Typs $f(x)= \frac{k}{x}$ (Funktion der indirekten Proportionlität).
Wenn wir wieder für $G$ die Gravitationskonstante einsetzen, für $M$ die Erdmasse und für $m =1$kg wählen, dann beschreibt diese Funktion die Abnahme des Gewichts mit zunehmendem Abstand von der Erde. (Hinweis: im Inneren der Erde nimmt die Gravitationskraft allerdings linear ab!)
Genauso könnten wir weitere sinnvolle Funktionen finden, etwa $F(G), F(M)$ , …$
Aufgabe TM5-837
Die Weltbevölkerung ist im 20. Jahrhundert stark gewachsen:
| Jahr | Anzahl in Mrd. |
| 1900 | 1,7 |
| 1950 | 2,6 |
| 2000 | 6,1 |
a) Erstelle mit den Angaben von 1950 und 2000 ein lineares Modell und stelle es graphisch dar.
b) Benutze alle Angaben, um die Zunahme der Weltbevölkerung durch ein quadratisches Modell zu beschreiben. Stelle dieses Modell für 1950 bis 2050 grafi sch dar.
c) Verwende beide Modelle, um eine Prognose für das Jahr 2030 abzugeben.
Ausführung mit GeoGebra
Hinweise:
Trage in der Tabellenansicht die gegebenen Werte ein.
Markiere diese Werte und erzeuge (über Rechtsklick) eine Liste von Punkten.
Mit dem Befehl Trendlinie[{B,C}] kannst du eine lineare Funktion erhalten, deren Graph genau durch die Punkte B und C verläuft.
Mit dem Befehl TrendPoly[{A,B,C},2] kannst du eine quadratische Funktion erhalten, die genau durch die vorgegebenen Punkte verläuft. Der Parameter 2 gibt dabei den Grad der Polynomfunktion an (quadratische Funktionen sind ja Polynome vom Grad 2).
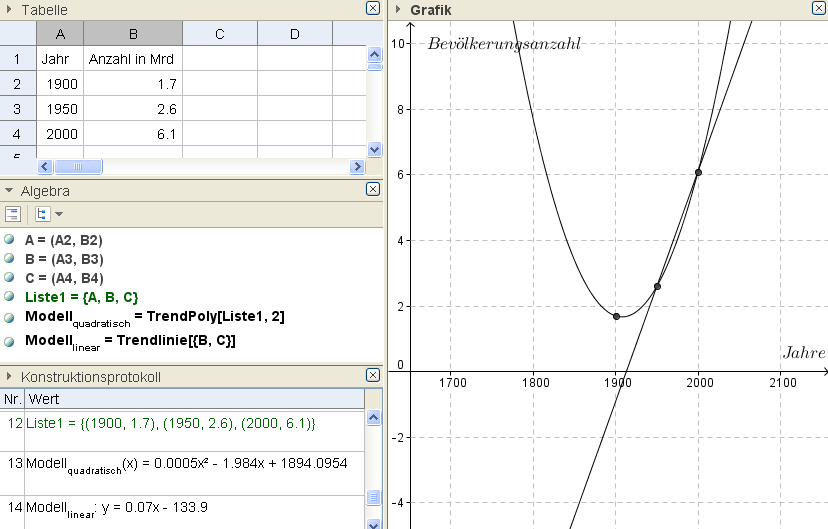
Durch Einsetzen in die beiden Funktionen erhalten wir für das Jahr 2030 die Werte 8,2 Mrd.(lineares Modell) bzw. 9,448 Mrd. (quadratisches Modell).
Vorsicht: beide Modelle besitzen nur einen sehr eingeschränkten Gültigkeitsbereich (bessere Modelle werden wir in der 6. Klasse erstellen).