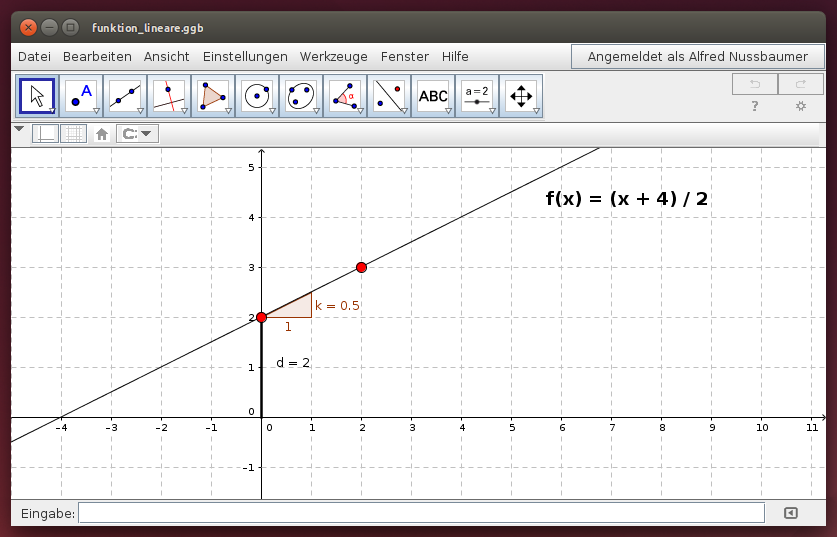
Inhomogene lineare Funktion
Verschiebe den roten Punkt auf der y-Achse und den zweiten roten Punkt. Vergleiche die angegebene Funktionsgleichung mit der Lage des Funktionsgraphen!
Aufgaben:
- Fasse Eigenschaften der inhomogenen linearen Funktion zusammen!
- Beschreibe die Bedeutung des Durchstoßpunkts durch die y-Achse und die Bedeutung des Steigungsdreiecks!
- Untersuche die Funktionsgleichung und die Funktionsgraphen, wenn der zweite Punkt der Geraden in den vier Quadranten des Koordinatensystems liegt: Wie hängt die Funktionsgleichung davon ab?
- Stelle inhomogene lineare Funktionen mit dem obigen GeoGebra-Applet dar, deren Eigenschaften stark voneinander abweichen!
Zurück zu Lineare Funktionen