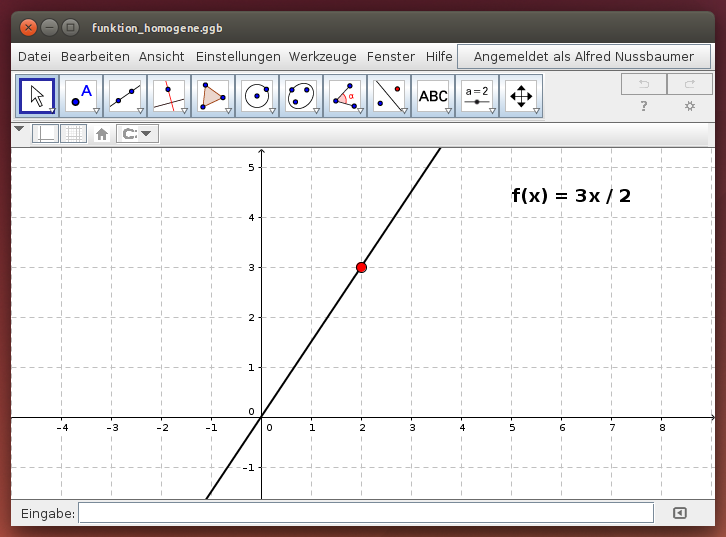
Homogene lineare Funktion
5, S. 110 - 111, BIFIE GK FA2.6
Verschiebe den roten Punkt und vergleiche die angegebene Funktionsgleichung mit der Lage des Funktionsgraphen!
Aufgaben:
- Fasse Eigenschaften der homogenen linearen Funktion zusammen!
- Wie ändert sich die Funktionsgleichung, wenn der rote Punkt der Reihe nach in den vier Quadranten des Koordinatensystems zu liegen kommt? Stelle eine Tabelle für alle Möglichkeiten auf!
- Stelle homogene lineare Funktionen mit dem obigen GeoGebra-Beispiel dar, deren Eigenschaften stark voneinander abweichen!
- Gib an, wie die Direkte Proportionalität durch eine homogene lineare Funktion beschrieben wird!
Zurück zu Lineare Funktionen
