Fortlaufende Potenzen reeller Zahlen
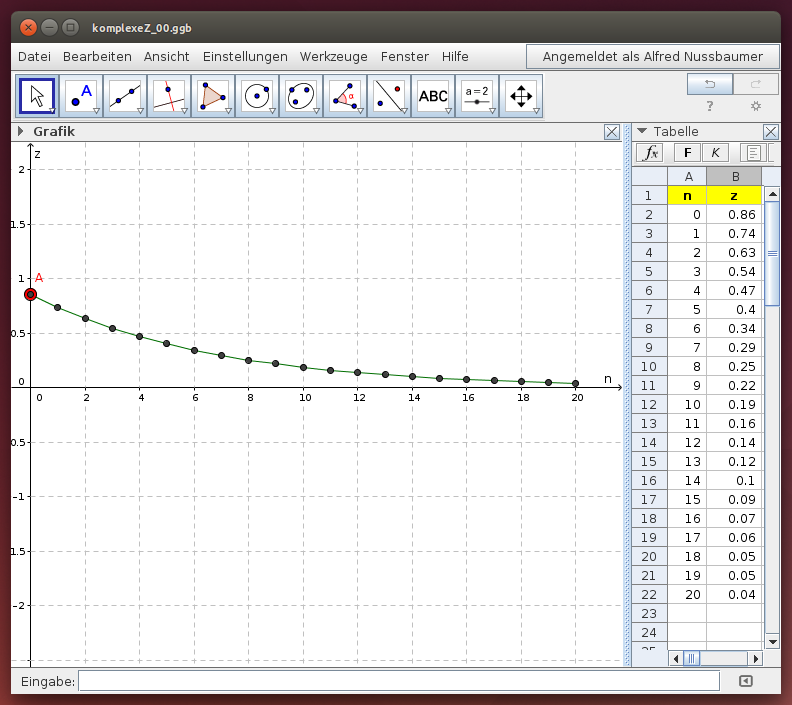
Die Potenzen z, z2, z3, z4, … reeller Zahlen können rekursiv oder explizit berechnet werden. Untersuche die Eigenschaften der Zahlenfolge in Abhängigkeit zum Folgenindex n: Im folgenden GeoGebra-Applet werden die ersten 20 Folgenglieder über der waagrechten Achse n dargestellt.
Wähle den Startwert z für die Folge, indem du den roten Punkt A auf der vertikalen z-Achse verschiebst und beobachte das Verhalten der Zahlenfolge:
Aufgaben:
- Gib an, unter welchen Bedingungen die Zahlenfolge z, z2, z3, z4, … konvergiert und unter welchen Bedingungen sie divergiert!
- Gib an, für welchen Spezialfall eine konstante Folge entsteht!
- Gib an, unter welchen Bedingungen einen alternierende Folge vorliegt!
- Suche einen „Spezialfall“ für eine alternierende Folge und beschreibe diesen Fall detailliert!
- Vergleiche mit den fortlaufenden Potenzen komplexer Zahlen (Lernpfad Komplexe Zahlen)!
- Zusatz: Gib eine explizite Formel für die Folge z, z2, z3, z4, … an!
Zurück zu Lernpfad Komplexe Zahlen | Komplexe Zahlen und algebraische Gleichungen