(zu )

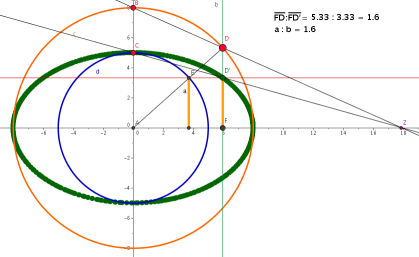
Affine Abbildungen (der Ebene auf die Ebene) haben drei bemerkenswerte Eigenschaften:

• Sie sind geradentreu (die Bilder zweier Punkte, die auf einer Geraden liegen, liegen ebenfalls auf einer Geraden)
• Sie sind parallelentreu (Bilder paralleler Geraden sind ebenfalls parallel)
• Sie sint teilverhältnistreu (Teilverhältnisse bleiben bei der Abbildung erhalten)

Darüber hinaus können Affine Abbildungen weitere Eigenschaften aufweisen. Sie sind im Allgemeinen aber

• nicht winkeltreu
• nicht längentreu
• nicht flächentreu
• nicht verhältnistreu
• nicht kreistreu

GeoGebra unterstützt dich bei folgenden Abbildungen - untersuche ihre Eigenschaften!

Hinweis: Die Spiegelung an einem Kreis (Inversion) ist nicht geradentreu, daher ist sie insbesondere auch keine affine Abbildung. Nichtsdestoweniger hat diese Abbildung interessante Eigenschaften und Gesetzmäßigkeiten!

Wenn du die Größe von Bildern am PC (Textverarbeitung, Präsentationssoftware, …) bearbeitest, führst du häufig affinde Abbildungen aus. Vergleiche mit den folgenen Beispielen der Abbildungsgeometrie!

• Schiebung
• Geradenspiegelung
• Punktspiegelung
• Drehung
• Zentrische Streckung
• Affine Abbildung eines Kreises auf eine Ellipse

Mit den Methoden der linearen Algebra lassen sich affine Abbildungen berechnen. Dabei rechnen wir mit linearen Gleichungssystemen. Der Übersichtlichkeit halber und wegen weiterer Vorzüge ist es üblich, statt der Gleichungssysteme mit Matrizen zu rechnen.