(zu 7)

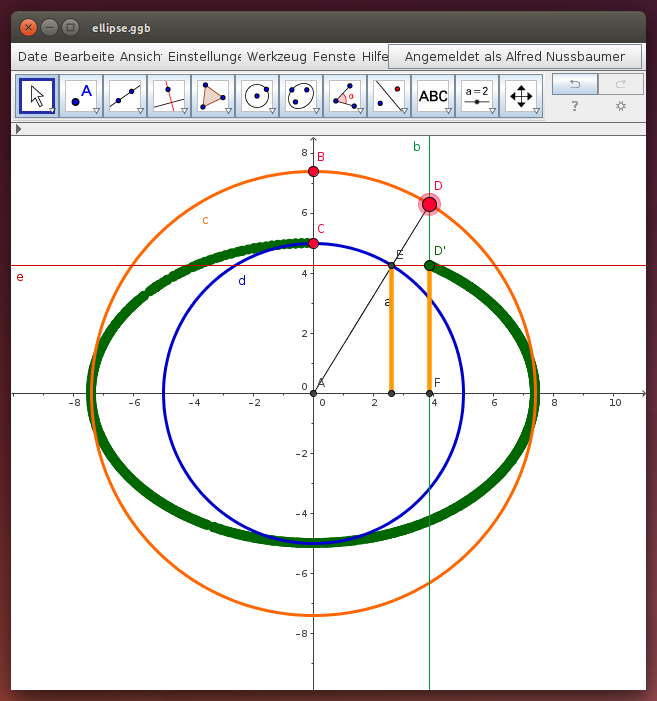
Gegeben sind zwei konzentrische Kreise in Mittelpunktslage. Der äußere Kreis wird auf eine Ellipse abgebildet, deren große Halbachse a dem Radius R des äußeren Kreises und deren kleine Halbachse b dem Radius r des inneren Kreises entspricht. Wir erzeugen die Ellipse, indem wir viele Punkte des äußeren Kreises folgendermaßen auf einen Punkt der Ellipse abbilden:

1. Wähle einen Punkt D auf dem äußeren Kreis
2. Dieser Punkt D und der Punkt D' auf der Ellipse haben die gleiche x-Koordinate (D' liegt „senkrecht“ unterhalb D).
3. Zeichne den Radius(vektor) und schneide ihn mit dem inneren Kreis
4. Die y-Koordinate dieses Schnittpunkts ist gleich der y-Koordinate des Ellipsenpunktes D'.

Verschiebe den Punkt D auf dem äußeren Kreis und beobachte die Spur des Punktes D':

Hinweis: Mit Strg-F kannst du die „Ansicht auffrischen“ - damit verschwinden schon bestehende Spuren.

Download der GeoGebra-Datei

Der Punkt D wird auf den Punkt D' abgebildet, konkret wird dabei die y-Koordinate des Punktes D verkürzt. Das Verkürzungsverhältnis ist genau das Verhältnis des Radius R des äußeren Kreises zum Radius r des inneren Kreises.

1. Wähle die Radien der beiden konzentrischen Kreise, indem du die Punkte B und C auf der senkrechten Koordinatenachse verschiebst!
2. Leite die Gleichung der Ellipse her!
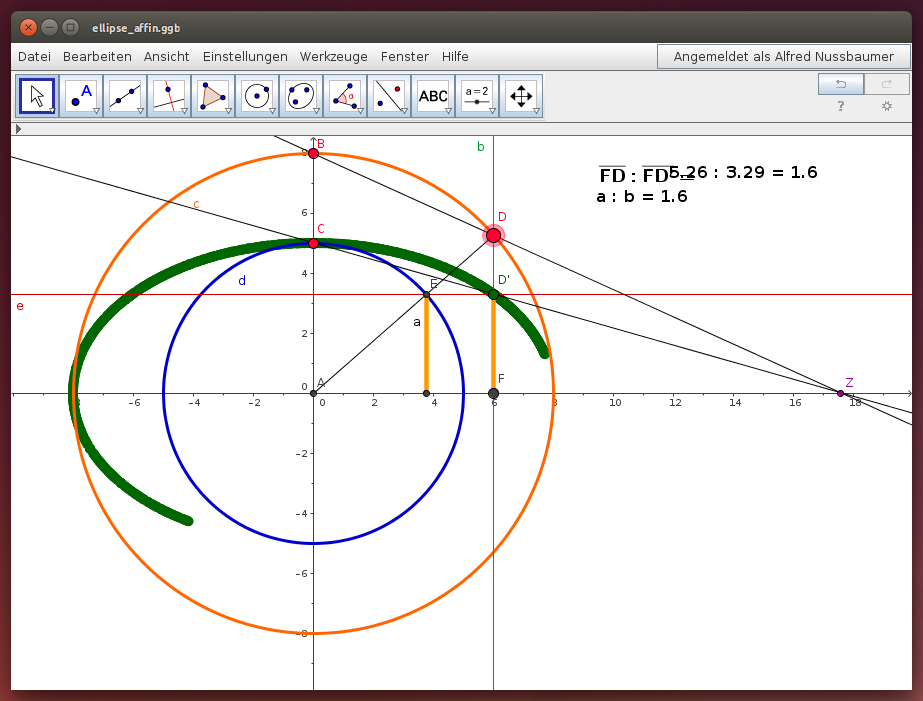
3. Untersuche die Eigenschaften der affinene Abbildung im folgenden GeoGebra-Applet

Download der GeoGebra-Datei

1. Was sind in der obigen Abbildung Fixgeraden und Fixpunkte?
2. Woran ist die Geradentreue zu erkennen?
3. Welche Rolle spielt der Punkt Z?
4. Welche Gerade ist die Affinitätsachse?
5. Woran ist zu erkennen, dass die Abbildung nicht flächentreu, nicht winkeltreu und nicht kreistreu ist?

Ausblick: Affine Abbildung

zurück zu Ellipse | Nichtlineare analytische Geometrie R2