Drehung

(zu tm.jpg 6, S. 158 - 159)

Drehungen sind Abbildungen vom R2 in den R2. Für die Drehung um den Koordinatenursprung können die Koordinaten des gedrehten Punktes mit Hilfe von Matrizen leicht berechnet werden:

Für den Drehwinkel tex:\alpha verwenden wir die 2×2 Abbildungsmatrix tex:\left[ \matrix {\cos \alpha & - \sin \alpha , \sin \alpha & \cos \alpha} \right].

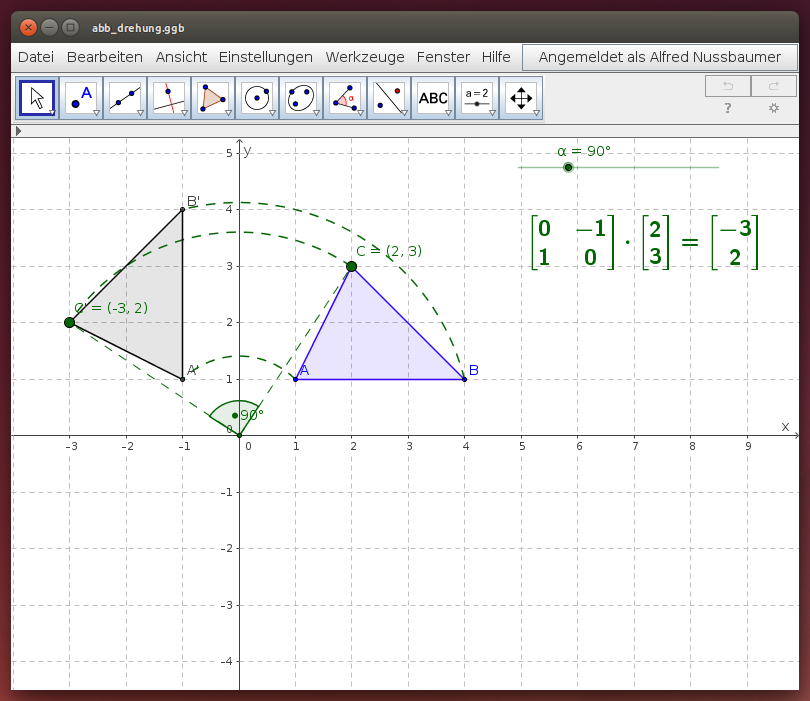
Mit dem folgenden GeoGebra-Beispiel kannst du Drehungen um 0°, 45°, 90°, … darstellen:

  1. Wähle einen Punkt C.
  2. Wähle einen Drehwinkel α mit dem Schieberegler.
  3. Lies die Koordinaten des gedrehten Punkts C' ab.
  4. Vergleiche mit der angegebenen Matrizenmultiplikation und rechne nach!

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Aufgaben:

  • Wähle drei Punkte A, B, C und einen Drehwinkel σ. Berechne anschließend mit der zugehörigen Abbildungsmatrix die Koordinaten der gedrehten Punkte A' und B' und vergleiche mit den Koordinaten aus dem GeoGebra-Beispiel!
  • Schreibe die Abbildungsmatrizen für die Drehung um 90°, 180°, 270° und 360° an: Welche Eigenschaften haben diese Matrizen gemeinsam?
  • Vergleiche mit den Abbildungsmatrizen für die Spiegelung an den Koordinatenachsen, 1. und 2. Mediane!
  • Vergleiche mit der Abbildungsmatrix für Streckungen und Skalierungen in x- und y-Richtung!
  • Öffne das GeoGebra-Beispiel und untersuche die Eigenschaften für ein allgemeines Fünfeck!

Ausblick: Affine Abbildung | Abbildungsgeometrie

Zurück zu geometrische Abbildungen | Koordinatensystem | Thema Symmetrie und Spiegelung | Reelle Funktionen | Matrizen


Zuletzt angesehen: • drehung