(zu 6, S. 158 - 159)

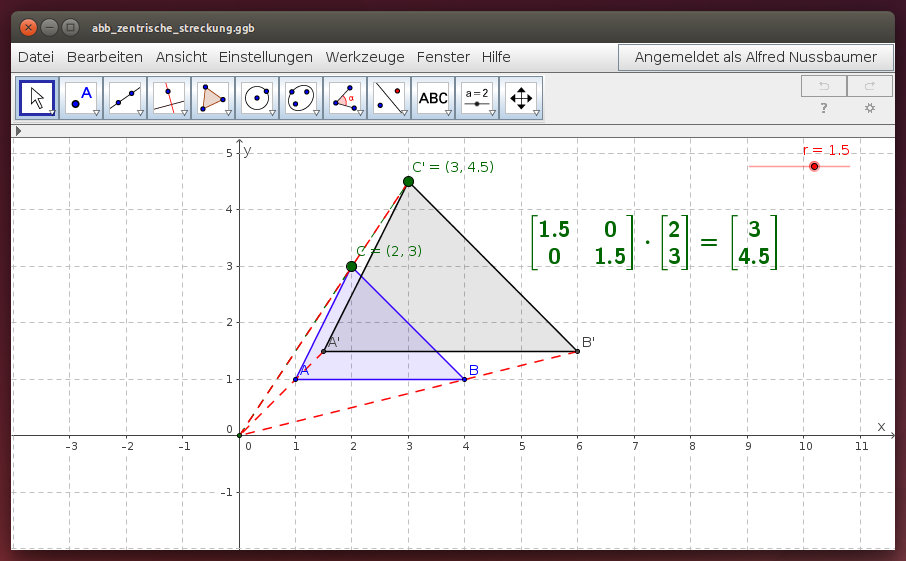
Beschreibe die Eigenschaften der zentrischen Streckung anhand des folgenden GeoGebra-Beispiels! Beachte insbesondere die Eigenschaften entsprechender Winkel und Strecken der Dreiecke A, B, C und A', B', C'. Wähle dazu verschiedene Streckungsfaktoren !

Download der GeoGebra-Datei

• Vergleiche die Eigenschaften der zentrischen Streckung mit den Aussagen des Strahlensatzes!
• Gib eine allgemeine Form für die Abbildungsmatrix an!
• Rechne nach: Werden die x- und die y-Achse mit dem Faktor r mutlipliziert, dann liegt ein Streckungsfaktor vor.
• Die zentrische Streckung ist ein Spezialfall der Drehstreckung. Beschreibe diesen Spezialfall!
• Wähle verschiedene Dreiecke A, B, C und überprüfe deine Vermutungen!
• Öffne das GeoGebra-Beispiel und untersuche die Eigenschaften für ein allgemeines Fünfeck!

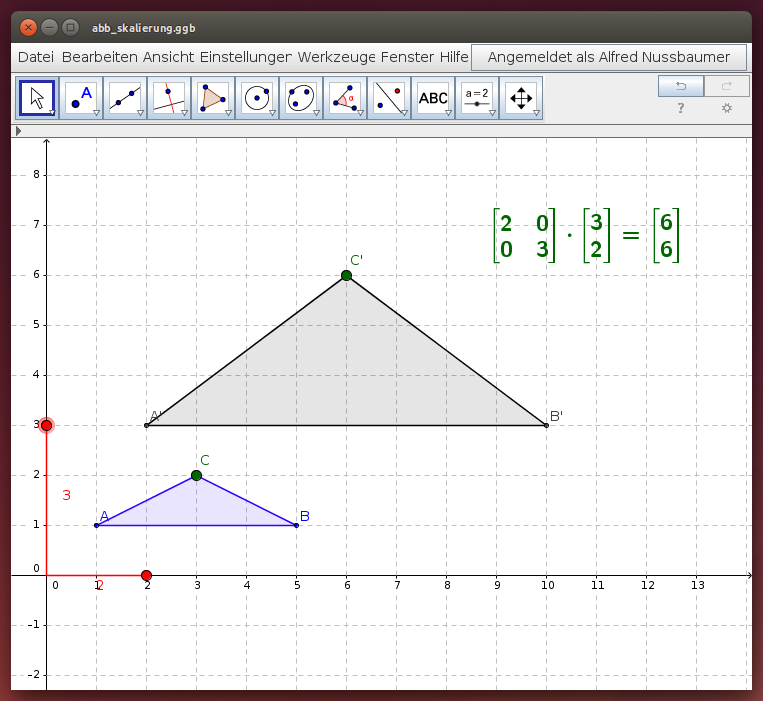
Wähle im folgenden GeoGebra - Beispiel die Skalierung in x-Richtung, indem du den roten Punkt auf der x-Achse verschiebst: Der Skalierungsfaktor entspricht dem Abstand vom Ursprung. Beobachte dabei die Formänderung für das Dreieck A'B'C'!

Verfahre ebenso für die Skalierung in y-Richtung!

Download der GeoGebra-Datei

• Für die Punkte C und C' wird die Berechnung mit Hilfe der Abbildungsmatrix dargestellt: Gib eine allgemeine Form der Abbildungsmatrix („Skalierungsmatrix“) für eine Skalierung in x-Richtung um den Skalierungsfaktor m an!
• Gib eine allgemeine Form der Skalierungsmatrix für die Skalierung in y-Richtung mit dem Skalierungsfaktor n an!
• Gib eine allgemeine Form der Skalierungsmatrix für die Skalierung in beiden Koordinatenrichtungen mit den Faktoren m und n an!
• Für welchen Spezialfall liegt eine zentrische Streckung vor?
• Wähle verschiedene Dreiecke A, B, C und überprüfe deine Vermutungen!
• Öffne das GeoGebra-Beispiel und untersuche die Eigenschaften für ein allgemeines Fünfeck!

Ausblick: Affine Abbildung | Abbildungsgeometrie

Zurück zu geometrische Abbildungen | Koordinatensystem | Thema Symmetrie und Spiegelung | Reelle Funktionen | Matrizen