Inhaltsverzeichnis
Lernpfad: Bestimmtes und unbestimmtes Integral
Bei zahlreichen „alltäglichen“ Situationen bilden wir Summen, wir „integrieren“, „kumulieren“ oder „berechnen Durchschnittswerte“. In diesem Lernpfad führen solche Situationen durch wesentliche Bereiche der Integralrechnung.
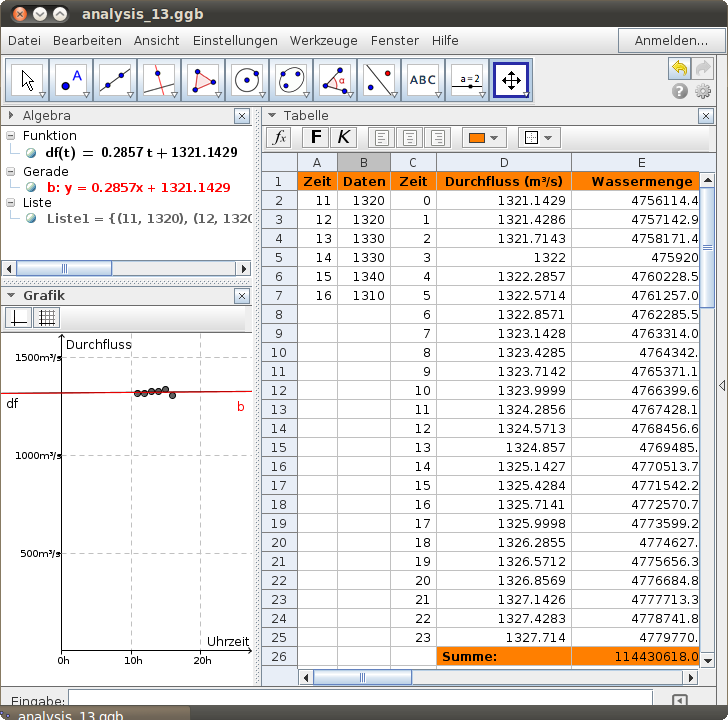
Durchfluss
Einer Wasserstandsliste werden die Daten für die Durchflussmenge (in m3/s) entnommen, und zwar für einen Zeitraum von 6 Stunden. Die Messungen um 11:00 Uhr, 12:00 Uhr, 13:00 Uhr, 14:00 Uhr, 15:00 Uhr und 16:00 Uhr werden mit einer Regressionsgerade zu Durchflussmengen zum jeweiligen Stundenbeginn während eines Tages genähert. Auf der Basis dieses Näherungswertes werden schließlich die Wassermenge pro Stunde berechnet und schließlich zur Wassermenge eines Tages aufsummiert.
Aufgaben:
- Beschreibe für eine eindimensionale Bewegung, von der der Geschwindigkeitsverlauf gegeben ist, den zurückgelegten Weg als Integral!
- Beschreibe die Berechnung der Viertelkreisfläche mit Hilfe von Rechteckstreifen!
- Beschreibe die Volumsberechnung einer Halbkugel mit Hilfe von Zylinderscheiben!
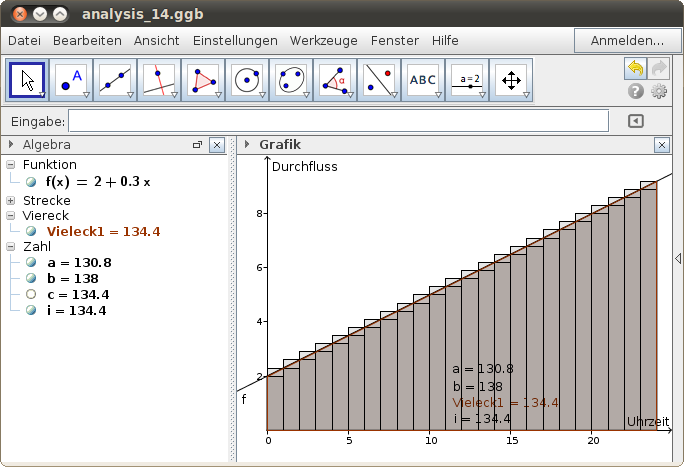
Modell: Flächeninhalt unter einer linearen Funktion
Wir wählen eine „idealisierte Regressionsgerade“ und berechnen die Produktsummen:
- Fall: Die Durchflussmenge pro Stunde zu Beginn einer Stunde wird mit einer Stunde multipliziert („Untersumme“).
- Fall: Die Durchflussmenge pro Stunde zum Ende einer Stunde wird mit einer Stunde multipliziert („Obersumme“).
- Wir bilden das „arithmetische Mittel“ von Ober- und Untersummen.
- Wir berechnen den Flächeninhalt des Trapezes („Vieleck“).
- Wir berechnen das „bestimmte Integral“ unter der Kurve.
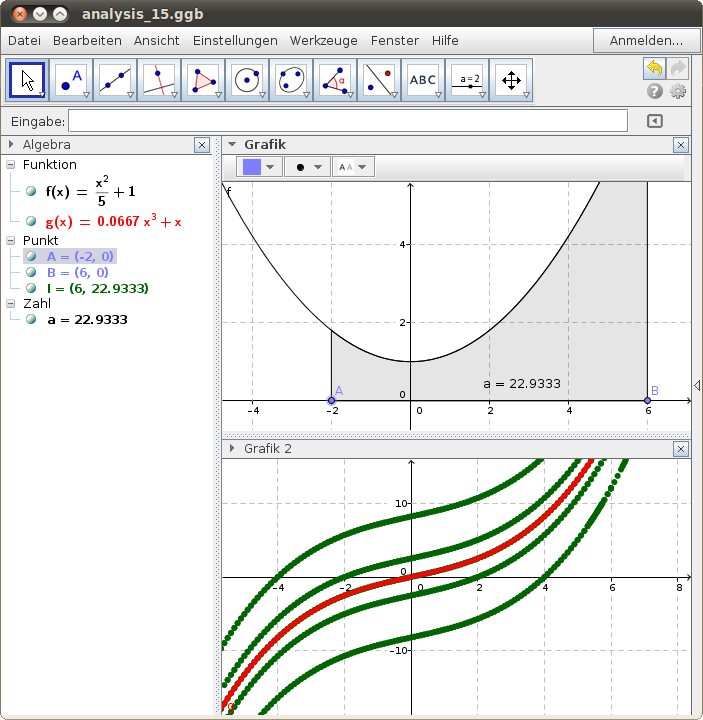
Grafisch eine Stammfunktion ermitteln
Wir berechnen den Flächeninhalt unter der Kurve mit dem GeoGebra-Befehl Integral(f,x(A),x(B)) und ordnen bei festem Punkt A die den jeweiligen Positionen des rechten Punktes B zugeordneten Flächeninhalte zu. Diese Ergebnisse stellen wir als Punktespur in einem 2. Grafikfenster dar:
Hinweis: Je nach der Lage des linken Endpunktes A erhalten wir eine andere Punktespur (der Punkt A ist somit eine Anfangsbedingung für unsere Ergebnisse).
- Grafisch eine Stammfunktion bestimmen (mit Hinweisen zur Arbeit mit GeoGebra
Aufgaben:
- Vergleiche das „grafische Integrieren“ mit dem grafischen Ableiten einer Funktion!
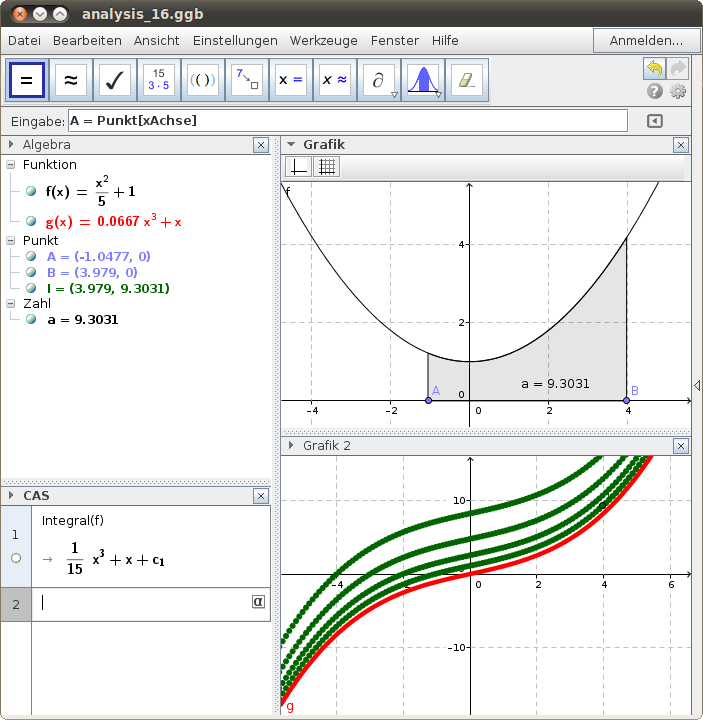
CAS: Bestimmen von Stammfunktionen
In der CAS-Ansicht erhalten wir das unbestimmte Integral - die Stammfunktion ist bis auf die Konstante gegeben.
Aufgabe:
- Rechne nach, dass die Ableitung des unbestimmten Integrals die Funktion ergibt („Ableiten“ und „Integrieren“ sind entgegengesetzte Rechenoperationen)!
Integrationsregeln
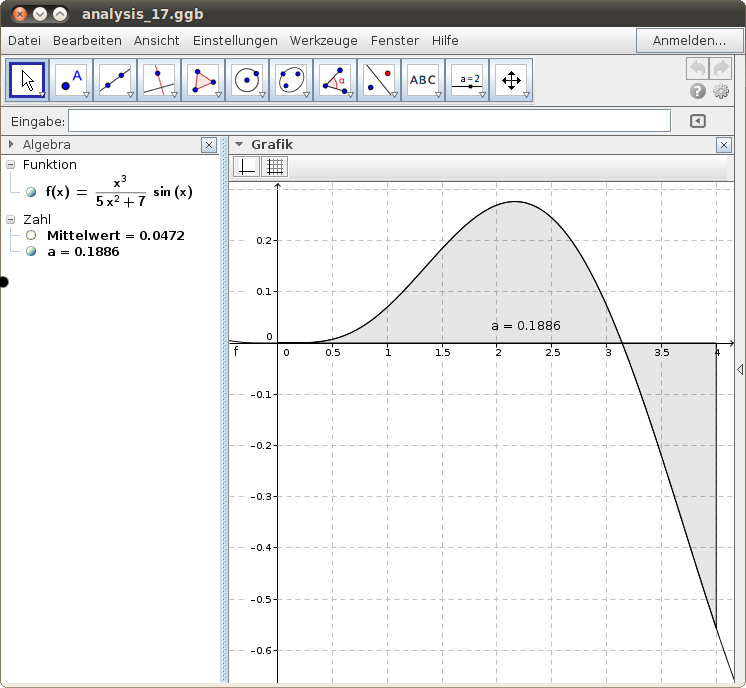
Anwendung: Der Mittelwert einer Funktion
Im abschließenden Beispiel berechnen wir den Mittelwert einer Funktion. Die Funktion f modelliert den Gewinn / Verlust bei einem Projekt in Millionen EUR pro Stück. Es werden 1, 2, … 4 Millionen Stück verkauft, wobei ab etwa 3 Millionen Stück ein immer größer werdender Verlust einsetzt. Berechne den Gesamtgewinn und den Mittelwert pro 1 Million Stück!
Zurück zu 8. Klasse | Bestimmtes Integral | Stammfunktion