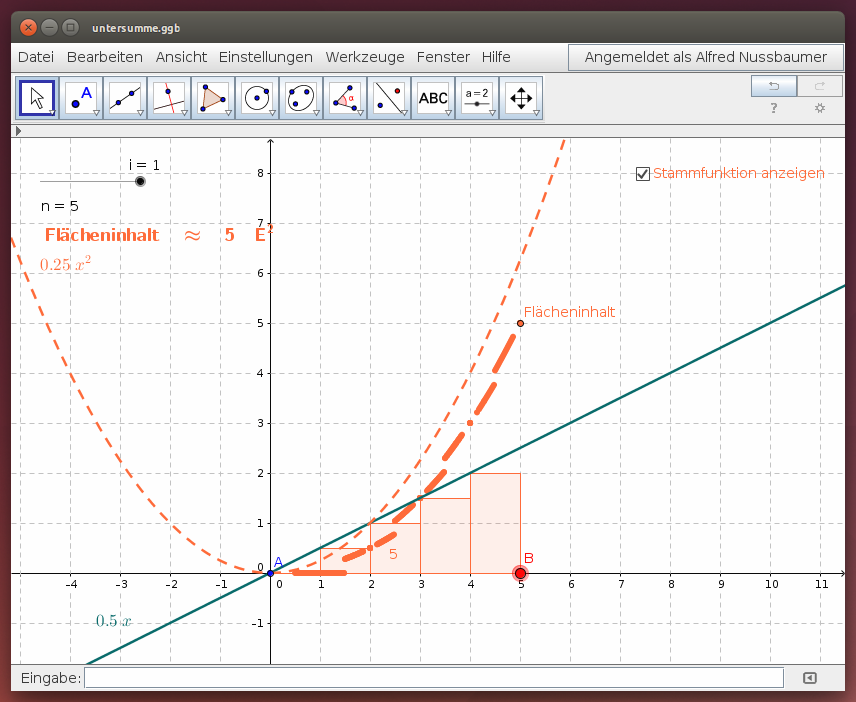
Untersumme
Wir berechnen den Flächeninhalt unter einer Kurve näherungsweise dadurch, dass wir die Fläche mit gleich breiten Rechteckstreifen auslegen. Die Rechteckstreifen reichen nicht über den Funktionsgraphen hinaus - es liegt eine Untersumme vor.
Variiere im folgenden GeoGebra-Applet die Streifenbreite i mit dem Schieberegler und interpretiere die Ergebnisse!
Aufgaben:
- Vergleiche mit der Obersumme!
- Verschiebe die rechte Intervallgrenze B und interpretiere die Punktespur für die Untersumme!
- Für Fortgeschrittene: Zeige die Stammfunktion (mit Hilfe des Kontrollkästchens) an und interpretiere die Abweichung der Punktespur!
Zurück zu Alternative Lösungswege | Grundlagen der Integralrechnung | Lernpfad Das bestimmte Integral | AN4.1