(zu 7)

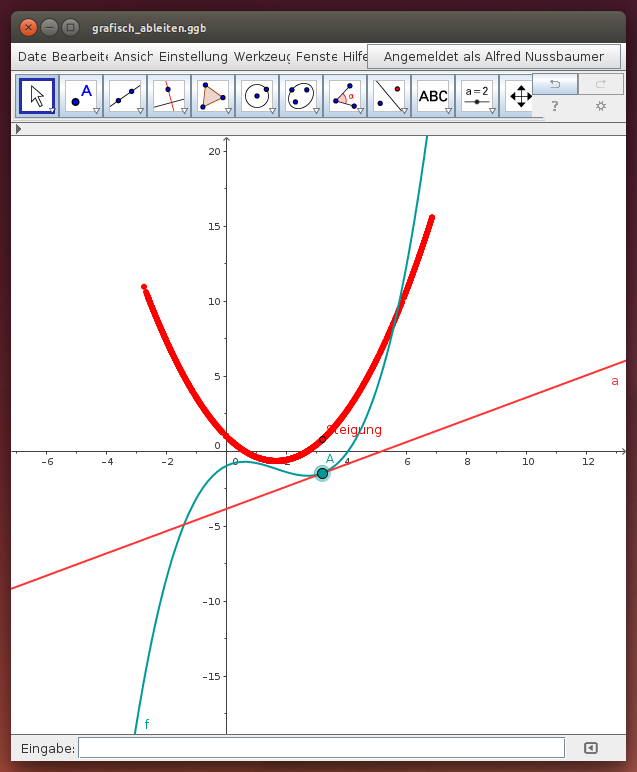
Im folgenden GeoGebra-Applet kannst du die Bedeutung der Ableitung einer Funktion „Punkt für Punkt“ untersuchen. Die Tangente an eine (im Beispiel blau dargestellte) Funktion hat im gewählten Punkt A eine bestimmte Steigung. Diese wird im Diagramm ebenfalls (rot) eingetragen.

Zu jeder x-Koordinate jedes Punktes einer differenzierbaren Funktion kann auf diese Weise die Steigung seiner Tangente an die Funktion ermittelt und gezeichnet werden. Wir erhalten eine Funktion aller Tangentensteigungen. Diese wird Ableitungsfunktion genannt:

Download der GeoGebra-Datei

1. Verschiebe den Punkt A auf dem gegebenen Funktionsgraphen und beobachte die Steigung der Tangente sowie die im Koordinatensystem aufgezeichneten Steigungs-Werte!
2. An welchen Stellen ist die Tangentensteigung Null?
3. In welchen Bereichen ist die Tangentensteigung positiv?
4. In welchen Bereichen ist die Tangentensteigung negativ?
5. Beschreibe die Eigenschaften der roten Kurve (= des Funktionsgraphen aller Tangentensteigungen) und vergleiche mit den Eigenschaften der gegebenen (blau dargestellten) Funktion! Mache Aussagen wie: „Hat die (rote) Ableitungsfunktion den Wert 0, dann hat die (blaue) Funktion an dieser Stelle …“
6. Öffne das GeoGebra-Applet mit einem Doppelklick und gib andere Funktionen f(x) in der Eingabezeile ein (zB f(x) = x^2 - 1, f(x) = sin(x), …)!

Zurück zu Grundlagen der Differentialrechnung | AN3.2