Mittelwert einer Funktion

Der arithmetische Mittelwert einer Datenreihe ist gegeben durch $tex:\frac 1 n \cdot \sum_{i=1}^n x_i$ . Liegen gleiche Werte tex:x_i vor, vereinfacht sich die Berechnung zu $tex:\frac 1 n \cdot \sum_{i=1}^k a_i x_i$ , wobei $tex:n = \sum k_i$ .

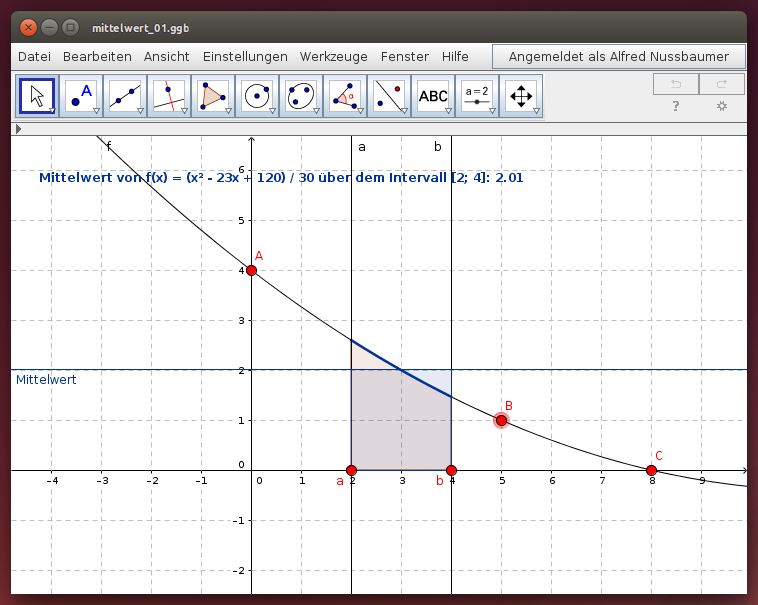
Liegen die Werte nicht diskret in Form einer Tabelle sondern kontinuierlich in Form eines Funktionsgraphen vor, wird aus der endlichen Summe von Produkten eine Summe von vielen kleinen Produkten; wir erhalten für den Mittelwert einer Funktion auf dem Intervall [a; b] die Formel $tex:\frac 1 {b - a} \int_a^b f(x) dx$ .

Download der GeoGebra-Datei

Aufgaben:

Variiere die Intervallgrenzen und beobachte den Mittelwert!
Wähle quadratische Funktionen, indem du die Punkte A, B oder C verschiebst und beobachte den Mittelwert!
Zeige, dass der Mittelwert einer Funktion für äquidistante Werte dem arithmetischen Mittelwert entspricht!
Vergleiche mit dem Mittelwertsatz der Integralrechnung!

Zurück zu Anwendungen der Integralrechnung | AN4.3

Zuletzt angesehen: • mittelwert_einer_funktion

Mittelwert einer Funktion

Aufgaben:

Navigation

Suche