Räumliche Koordinatengeometrie: Die xy-Ebene
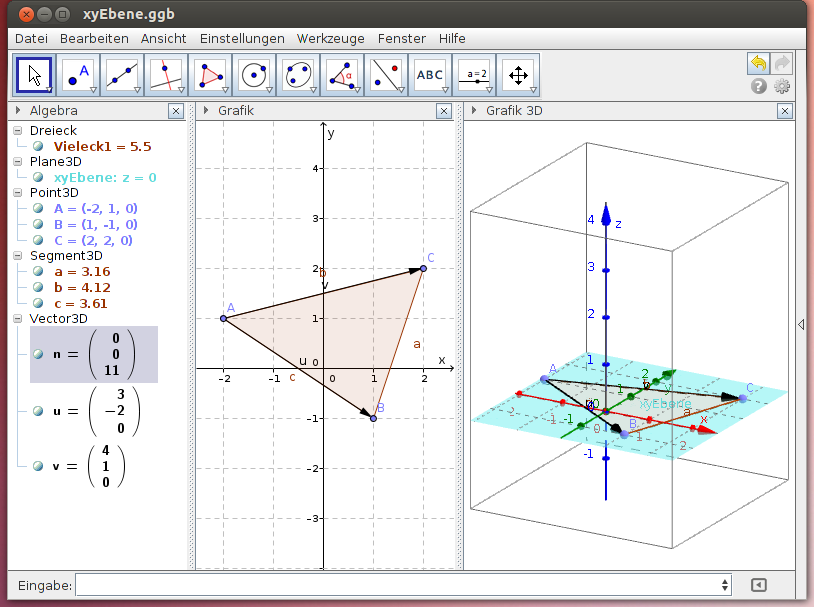
Die xy-Ebene enthält alle Punkte des Raumes, dessen z-Koordinate Null ist. Im folgenden GeoGebra-Beispiel legen die Punkte A, B und C ein Dreieck fest, das in der xy-Ebene liegt. Der Eckpunkt A und die Vektoren und
geben eine Parameterdarstellung der xy-Ebene an. Der Normalvektor
steht normal auf die xy-Ebene; er ist parallel zur z-Achse. Somit beschreibt die Gleichung
die xy-Ebene (vgl. die Normalvektorform der Ebenengleichung:
Aufgaben:
- Erstelle auf ähnliche Weise GeoGebra-Arbeitsblätter zur yz-Ebene und zur xz-Ebene!
- Vergleiche die Ebenengleichungen der xy-Ebene, der yz-Ebene und der xz-Ebene mit den Darstellungsformen in der 3D-Ansicht!
- Gib lineare Gleichungsysteme an, die die x-Achse, die y-Achse und die z-Achse im räumlichen Koordinatensystem festlegen!
Zurück zu Analytische Geometrie des Raumes | Schnitt: Zylinder und Ebene | Schnitt: Kegel und Ebene |