Lineare Gleichungssysteme mit zwei Variablen kannst du grafisch mit GeoGebra lösen. Für lineare Gleichungssysteme mit 3 und mehr Unbekannten verwendest du ein Computer-Algebra-System, z.B. GeoGebra CAS.

„Per Hand“ löst du lineare Gleichungssysteme mit 3 Unbekannten am besten mit dem Eliminationsverfahren oder mit Hilfe der Matrizenrechnung.

Zum Üben und Experimentieren findest du hier lineare Gleichungssysteme mit ganzzahligen Lösungen. Du kannst die Aufgaben „per Hand“ oder mit einem Computer-Algebra-System lösen…

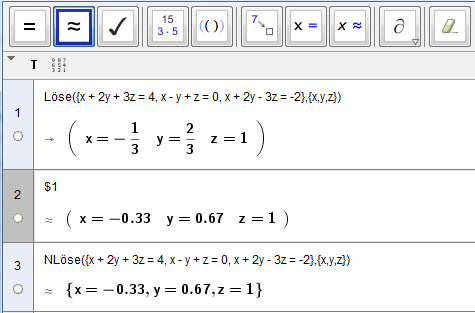
GeoGebra CAS: Löse(<Liste von linearen Gleichungen>,<Liste der Unbekannten>)

Beispiel: Löse das lineare Gleichungssystem x + 2y + 3z = 4, x - y + z = -1, x + 2y - 3z = 2!

Lösung:

6 S. 106 - 107

Die Ebenen e₁, e₂ und e₃ sind jeweils in Normalvektorform gegeben - jede Ebene wird durch eine lineare Gleichung mit den drei Unbekannten x, y und z festgelegt. Berechne die Koordinaten des gemeinsamen Schnittpunktes!

1. e₁: x + 2y - 3z = 1, e₂: x - y - z = 7, e₃: x + y - 2z = 0, Lösung: x = -10, y = -8, z = -9
2. e₁: x - 2y + 3z = 1, e₂: x - y + z = 7, e₃: x + y - 2z = 0, Lösung: x = -6, y = -32, z = -19
3. e₁: x - 2y + 3z = 1, e₂: x - y + z = 7, e₃: x + y + z = 3, Lösung: x = 9, y = -2, z = -41
4. e₁: 5x - y + 2z = 0, e₂: x - 2y + z = 0, e₃: 3x + 2y - z = -4, Lösung: x = -1, y = 1, z = 3
5. e₁: 3x - y + z = 0, e₂: x - 2y + z = 0, e₃: 3x + 2y - z = -4, Lösung: x = -1, y = 2, z = 5
6. e₁: 3x - y + z = 0, e₂: 2x - 2y + 3z = 1, e₃: 3x + 2y - 2z = 0, Lösung: x = 0, y = 1, z = 1
7. e₁: 2x + y + 3z = 0, e₂: x - 3y + 4z = 3, e₃: x - 2y - z = -15, Lösung: x = -7, y = 2, z = 4
8. e₁: 3x - y + 3z = 2, e₂: 3x - y + z = 1, e₃: x + 2y - 3z = 3, Lösung: x = 1, y = 1, z = 0
9. e₁: 2x - y + z = 1, e₂: x - 2y + z = 3, e₃: x + y - z = -1, Lösung: x = 0, y = -2, z = -1
10. e₁: 2x + 2y - z = 2, e₂: 2x + y + 3z = 0, e₃: 5x + 4y - 3z = 3, Lösung: x 0 -1, y = 2, z = 0

6 S. 102 - 103

Die Ebene e ist in Normalvektorform gegeben, die Gerade g wird durch eine Parameterdarstellung festgelegt. Das lineare Gleichungssystem mit den 4 Unbekannten t, x, y und z kannst du durch Substitution oder Elimination lösen - berechne die Koordinaten des Durchstoßpunktes!

1. g: X(t) = (3|2|1) + t (1|-5|2), e: x + y + z = 0, Lösung: t = 3, x = 6, y = -13, z = 7
2. g: X(t) = (1|2|0) + t (-1|3|2), e: x + y + z = -1, Lösung: t = -1, x = 2, y = -1, z = -2
3. g: X(t) = (3|1|4) + t (-1|3|2), e: x + y + 2z = 0, Lösung: t = -2, x = 5, y = -5, z = 0
4. g: X(t) = (3|2|1) + t (1|-5|2), e: x + y + z = 4, Lösung: t = 1, x = 4, y = -3, z = 3
5. g: X(t) = (-5|3|7) + t (1|-3|0), e: 2x - 3y + 7z = -14, Lösung: t = -4, x = -9, y = 15, z = 7

6 S. 104 - 105

Zwei Ebenen e₁ und e₂ sind in Normalvektorform gegeben. Berechne die Gleichung ihrer Schnittgeraden g (in Parameterform)!

1. e₁: 2x - 3y + z = -6, e₂: x + y - 2z = 2, Lösung: g: X(t) = (0|2|0) + t (1|1|1)
2. e₁: 2x - y + z = 0, e₂: x + y - z = 0, Lösung: g: X(t) = (0|0|0) + t (0|1|1)
3. e₁: 2x - 3y + z = -1, e₂: x + y - 2z = 2, Lösung: g: X(t) = (1|1|0) + t (1|1|1)
4. e₁: 2x + y + 5z = -6, e₂: x + y - 2z = 2, Lösung: g: X(t) = (-8|10|0) + t (-7|9|1)
5. e₁: 2x + y + 5z = -6, e₂: x - y - 2z = 0, Lösung: g: X(t) = (-2|-2|0) + t (-1|-3|1)

Zurück zu Gleichungen und Ungleichungen | Analytische Geometrie des Raumes | Lineare Gleichungssysteme