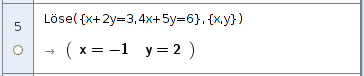Lösen von linearen Gleichungssystemen mit zwei Unbekannten

zu - Einstieg in die Oberstufe, S. 14 - 15, zu BIFIE GK AG2.5

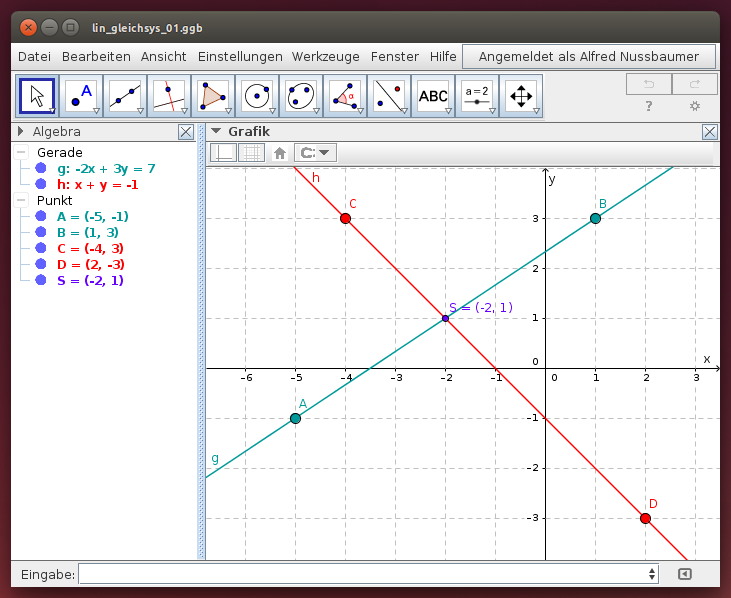
Lineare Gleichungssysteme mit zwei Unbekannten lassen sich leicht grafisch darstellen und lösen. Verwende dazu das folgende GeoGebra-Beispiel; du kannst es in zweierlei Hinsicht verwenden:

1. Ziehe die Geraden g:Gerade[A,B] mit Hilfe der Punkte A und B und h:Gerade[C,D] mit Hilfe der Punkte C und D in die gewünschten Positionen. Lies anschließend ihre Gleichungen aus dem Algebrafenster und ihre Lösung als Koordinaten des Schnittpunkts S ab!
2. Gib die linearen Gleichungen über die Eingabezeile ein, z.B.: g:x + 2y = 3 und h:4x + 5y = 6 und lies ihre Lösung wieder aus den Koordinaten des Schnittpunkts S ab!

Download der GeoGebra-Datei

Aufgaben:

• Gib an, bei welchen geometrischen Eigenschaften der beiden Geraden genau eine Lösung des zugehörigen linearen Gleichungssystems zu erwarten ist!
• Gib an, bei welchen geometrischen Eigenschaften der beiden Geraden keine Lösung des zugehörigen linearen Gleichungssystems zu erwarten ist!
• Gib an, bei welchen geometrischen Eigenschaften der beiden Geraden unendlich viele Lösungen des zugehörigen linearen Gleichungssystems zu erwarten sind!

In den folgenden Aufgaben wiederholst du die Lösungsverfahren durch Substitution, Gleichsetzen und Eliminieren. Die Aufgaben sind so gestellt, dass du sie im Kopf lösen kannst - du darfst aber auch mit Zettel und Bleistift rechnen!

• Löse das Gleichungssystem durch Substitution!
• Löse das Gleichungssystem durch Substitution!

• Löse das Gleichungssystem durch Gleichsetzen!
• Löse das Gleichungssystem durch Gleichsetzen!
• Löse das Gleichungssystem durch Gleichsetzen!

• Löse das Gleichungssystem durch geschicktes Eliminieren!
• Löse das Gleichungssystem durch geschicktes Eliminieren!

Beispiel: Löse das lineare Gleichungssystem x + 2 y = 3, 4 x + 5 y = 6!

Lösung:

Sonderfälle

Zurück zu Gleichungen und Ungleichungen