ab_gleich04 - Ma::Thema::tik

Arbeitsblatt: Bruchgleichungen

(zu 5, S. 84 - 85)

Lernziele: Eine Bruchgleichung erkennen und durch Multiplikation mit dem Hauptnenner umformen können; die Definitionsmenge und zutreffende Lösungen angeben können.
Überblick, Recherche: 5, S. 84 - 85, Gleichungen
Hilfsmittel: Computer-Algebra-System, GeoGebra, „Zettel und Bleistift“

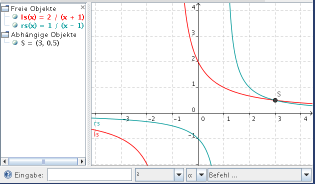Verwende auch die grafische Darstellung der beiden Seiten einer Bruchgleichung!

Skizziere die Vorgangsweise beim Lösen von Bruchgleichungen in einigen Schritten!

Achte bei allen Bruchgleichungen auf die Definitionsmenge! Beachte, dass Quadrate und höhere Potenzen der Unbekannten x wegfallen.

$tex:\frac 2 {x+1} = \frac 1 {x-1}$ , Lösung: x = 3
$tex:\frac 1 {x+1} = \frac 2 {x-3}$ , Lösung: x = -5
$tex:\frac 5 {2x + 3} = \frac 2{3x-1}$ , Lösung: x = 1
$tex:\frac 1 {x+4} - \frac 2 {x-3} = 0$ , Lösung: x = -11
$tex:\frac 1{x-1} + \frac 1 {x+1} = \frac {x^2 + 3}{x^2-1} - 1$ , Lösung: x = 2
$tex:\frac x {x+1} = \frac 5 {2x + 2} + \frac {2x}{x+2} - 1$ , Lösung: x = 6
$tex:\frac 3 {x-7} = \frac 4 {x+2} + 1 - \frac {x^2}{(x-7)(x+2)}$ , Lösung: x = -12
$tex:\frac x {1-x} + \frac 3 {2 - x} = \frac 1 {(1-x)(x-2)} - 1$ , Lösung: x = 3/2
$tex:\frac x {x+1} - x = \frac 1 {x-1} + \frac 1 {x+1}$ , Lösung: x = 0
$tex:\frac x {x-1} = 3 + \frac 1 {x-3}$ , Lösung: x = 2
$tex:\frac 1 {x-1} + \frac 1 {x+1} = \frac x {x+1}$ , Lösung: x₁ = 0, x₂ = 3

Gib an, auf welche Weise du die obigen Gleichungen sicher und vorteilhaft gelöst hast! Vielleicht kannst du auch „Tipps“ angeben.

Zuletzt angesehen: • ab_gleich04