Logistisches Modell
Das logistische Modell kombiniert das exponentielle und das beschränkte Modell: Die absolute Änderung ist in gleichen Zeitabschnitten proportional zum aktuellen Wert und zum Rest.
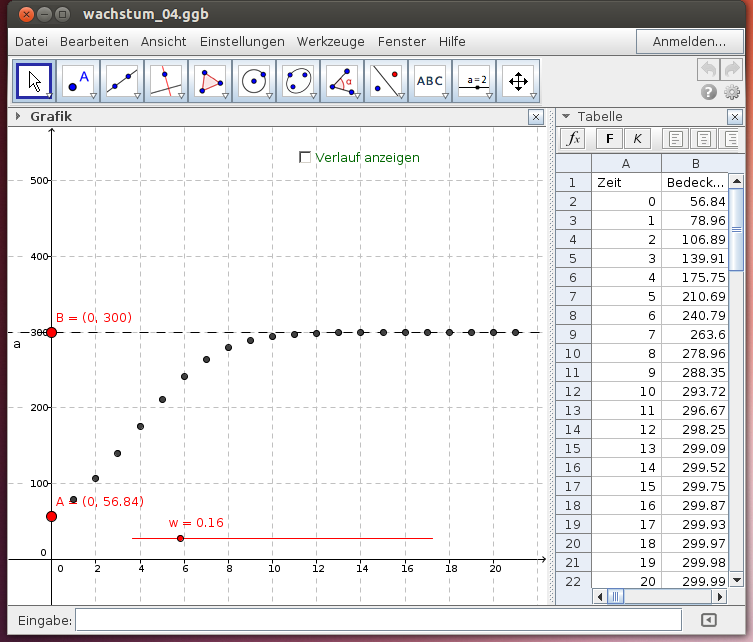
Im folgenden GeoGebra-Beispiel startet das Wachstum zum Zeitpunkt 0 mit dem Wert A, die Änderung in jedem Zeitschritt ist einerseits proportional zum aktuellen Wert und zum noch freien Bereich der Wasseroberfläche.
Aufgaben:
- Gib die Formel zur Berechnung der Wachstumskurve in der Tabellenspalte B an!
- Wähle verschiedene Anfangswerte A und interpretiere den Verlauf der Wachstumskurve!
- Wähle verschiedene Grenzwerte B (Ausdehnung der Wasseroberfläche) und interpretiere den Verlauf der Wachstumskurve!
- Begründe, warum dieses Modell zunächst ein exponentielles, dann aber ein beschränktes Wachstum zeigt!
- Gib die Differenzengleichung an!
- Wähle verschiedene Wachstumsraten w und interpretiere den Verlauf der Wachstumskurve!
Hinweis: Die Wachstumskurve hängt sehr empfindlich von der Wahl für w ab! Ab einem Wert von w erhalten wir mehrere Häufungswerte (Grenzwerte), für noch größere Werte verhalten sich die Werte chaotisch … Zeige in diesen Fällen den Verlauf an (Kontrollkästchen)!
Zurück zu Modelle | AN1.1 | AN1.2 | AN1.4 | Weiter zu Feigenbaumdiagramm