Logistisches Wachstumsmodell

tm.jpg 8, S. 122 - 123

Screenshot: A. NussbaumerBeim logistischen Wachstumsmodell ist die (relative) Änderungsrate (der Zuwachs pro Zeitschritt) proportional zum aktuellen Bestand und proportional zur Differenz zwischen dem aktuellen Bestand und dem Grenzwert. Die zugehörige Differentialgleichung lautet somit:

tex:y(t) = k \cdot y(t) \cdot (G - y(t))

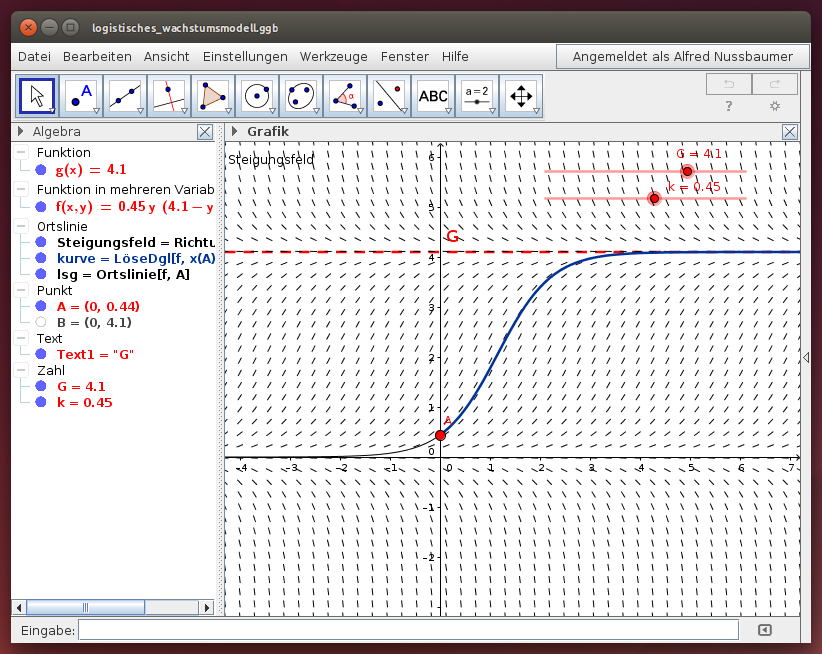
Die Lösungskurven werden im folgenden GeoGebra-Beispiel dargestellt:

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Aufgaben:

  • Variiere k und erkläre, wie die Lösung der Differentialgleichung tex:y'(t) = k \cdot y(t) \cdot (G - y(t)) von k abhängt!
  • Variiere den Anfangswert A und beschreibe, wie die Bestandsgröße y vom Anfangswert A abhängt!
  • Variiere den Grenzwert G und beschreibe, wie die Lösung der Differentialgleichung davon abhängt!
  • Stelle Richtungsfeld und die Lösungsfunktion durch den Anfangswert A für verschiedene Werte des Parameters k in Differentialgleichung tex:y'(t) = k \cdot y(t) \cdot (G - y(t)) dar! Wann liegt ein Wachstumsprozess, und wann liegt ein Zerfallsprozess vor?
  • Untersuche, wie die Lösungskurve von der Wahl des Anfangswerts A und von der Größe des Grenzwerts G abhängt!
  • Modelliere einen analogen diskreten Wachstumsprozess (z.B. mit Hilfe der Tabellenkalkulation)!

Zurück zu Dynamische Systeme

Weiter zu Lineares Wachstumsmodell | Exponentielles Wachstumsmodell | Beschränktes Wachstumsmodell | AN1.1 | AN1.2


Zuletzt angesehen: • logistisches_wachstumsmodell