Spinnwebdiagramm - logistisches Modell

tm.jpg 6, S. 180 - 181

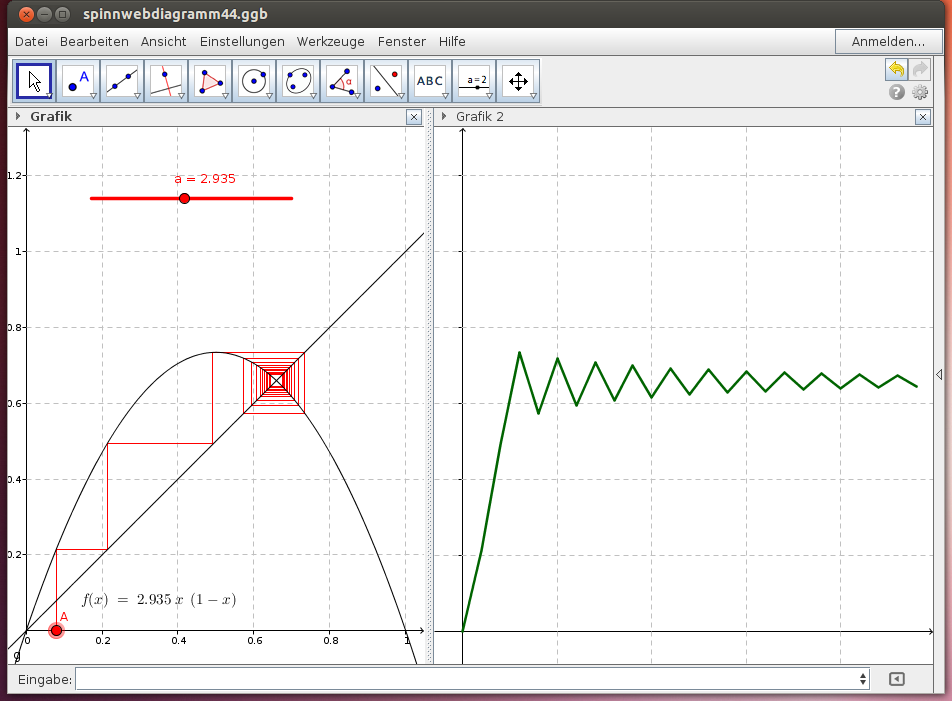
Die rekursive Abhängigkeit wird im folgenden GeoGebra-Beispiel durch die Funktion tex:y_{n+1}=a y_n (1 - y_n) definiert. Wähle den Startwert A und beobachte die zeitliche Abfolge der Funktionswerte tex:y_n im Zeitdiagramm!

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Aufgaben:

  • Verschiebe den Startpunkt „A“ horizontal auf der x-Achse und beobachte den Streckenzug des Spinnwebdiagrammes! Schreibe deine (vermuteten) Gesetzmäßigkeiten auf …
  • Die Rekursion ist durch die Funktion tex:f(x) = a \cdot x \cdot (1-x) und durch die 1. Mediane gegeben. Begründe!
  • Der Streckenzug im 2. Grafikfenster zeigt das Zeitverhalten der Werte tex:y_n. Beschreibe die Eigenschaften dieses Streckenzuges!
  • Was hat die Form der erhaltenen Kurven mit einem „Grenzwert“ zu tun?
  • Wähle verschiedene Werte für den Parameter a mit dem Schieberegler und beschreibe, wie die Form des Streckenzuges für tex:y_n vom Parameter a abhängt.

Ausblick:

Stellt man die Häufungspunkte der Werte von tex:y_n in Abhängigkeit vom Parameter a dar, so erhält man das Feigenbaumdiagramm.

Zurück zu Lernpfad Fraktale | Modelle | Weiter zum Feigenbaumdiagramm


Zuletzt angesehen: • wachstum_05