Exponentielles Modell
Beim exponentiellen Modell wächst die absolute Änderungsrate an, die relative Änderungsrate ist konstant („gleiche Zeitschritte - gleiche relative Änderungen“).
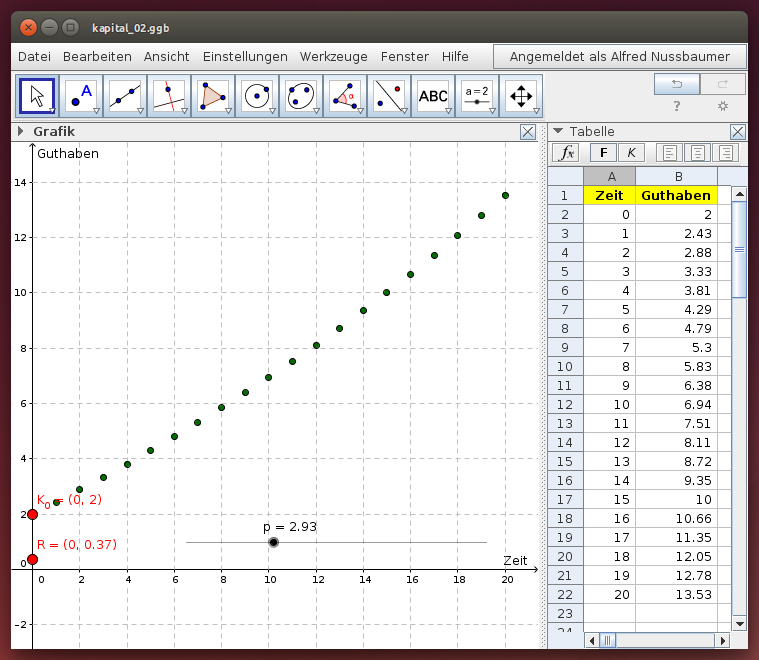
Im folgenden GeoGebra-Modell startet eine Kapitalisierung zum Zeitpunkt 0 mit dem Grundkapital K0, nach jedem Zeitschritt kommt die gleichbleibende Rate R dazu, außerdem wird das bestehende Kapital nach diesem Zeitraum entsprechend dem gewählten Zinssatz p um die Zinsen vermehrt:
Aufgaben:
- Für Werte der Rate R <> 0 liegt im obigen GeoGebra-Modell eine Kombination aus linearem Modell und exponentiellem Modell vor. Begründe!
- Gib die Formel zur Berechnung der Guthaben in der Tabellenspalte B an!
- Wähle verschiedene Grundkapitalwerte K0 und interpretiere den Verlauf der Kapitalkurve!
- Wähle verschiedene Raten R und interpretiere den Verlauf der Kapitalkurve!
- Wähle verschiedene Zinssätze p und interpretiere den Verlauf der Kapitalkurve!
- Wähle R = 0 und interpretiere die Kapitalkurve bei verschiedenen Zinssätzen p!
- Wähle einen negativen Wert für R: Was bedeutet das negative Vorzeichen? Zu welchem Zeitpunkt ist das Kapital auf Null gesunken?
- Begründe, warum dieses Modell ein exponentielles Modell ist!
- Gib die Differenzengleichung an!