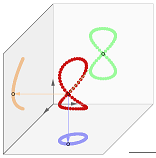
Die Viviani-Kurve
Eine Parameterdarstellung für die Viviani-Kurve mit Radius r = 1 lautet:
x(t) = cos(t)^2 y(t) = cos(t)*sin(t) z(t) = sin(t)
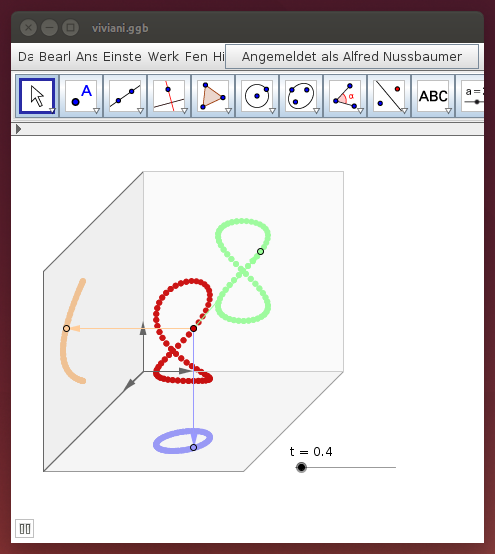
Verschiebe im folgenden GeoGebra-Applet den Regler für den Parameter t und beobachte die Lage des Punktes der Raumkurve und seine drei „Schatten“! Alternativ kannst du auch die Animation starten.
Aufgaben:
- Beschreibe die Formen der auf die drei Koordinatenebenen projizierten Kurve!
- Beobachte und beschreibe, wie oft die „Schattenkurven“ durchlaufen werden, wenn die Raumkurve einmal gezeichnet wird!
- Öffne das obige GeoGebra-Applet, variiere die Parameterdarstellung und beobachte ähnliche Kurven!
- Die Viviani-Kurve entsteht als Schnittkurve zwischen Kugel und Zylinder. Recherchiere dazu!
- Die Viviani-Kurve lässt sich als Ortslinie definieren. Recherchiere dazu!
- Vergleiche obige Parameterdarstellung der Viviani-Kurve mit folgender Definition der Viviani-Kurve:
x(t) = 1 + cos(t) y(t) = sin(t) z(t) = 2 sin (t/2)
Der Satz von Viviani bezieht sich auf gleichseitige Dreiecke (mehr dazu).
Zurück zu Parametrisierte Kurven | Kurven im Schrägriss | Schnitte von räumlichen Objekten | Lernpfad: GeoGebra - Grafik 3D