(zu )

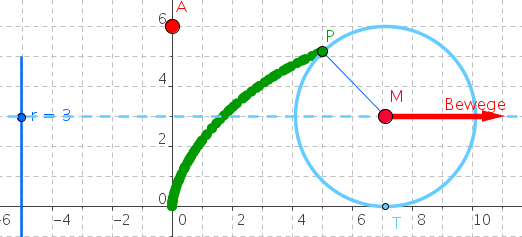
Die Zykloide wird deshalb Rollkurve genannt, weil sie die Bahn eines Punktes auf dem Kreisumfang beschreibt, wenn der Kreis waagrecht rollt.

http://de.wikipedia.org/wiki/Rollkurve

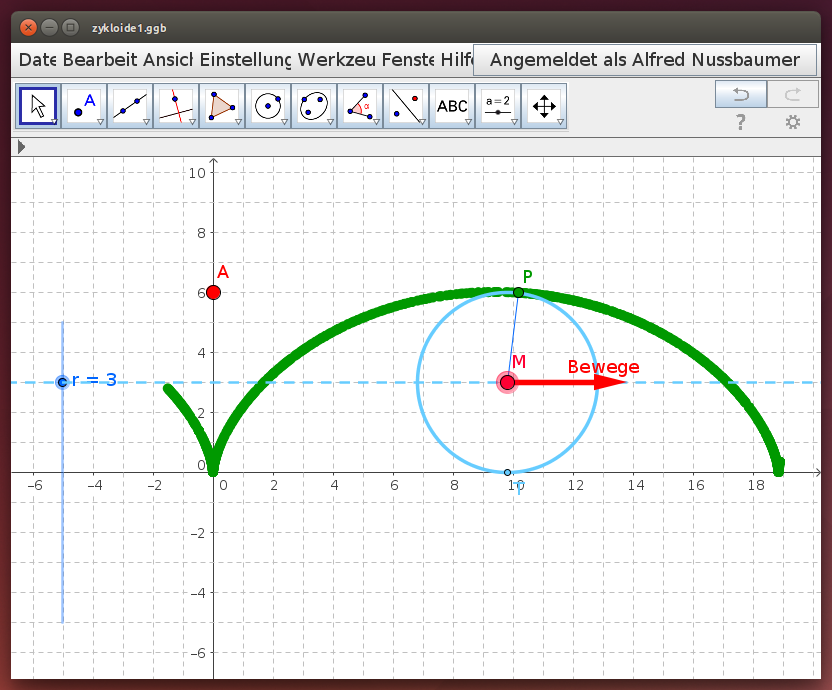
Mit dem folgenden GeoGebra-Applet kannst du diesen Vorgang im Detail erforschen - die Rollkurve wird als Spur des Punktes P sichtbar. Wähle den Durchmesser des abrollenden Kreises, indem du den Punkt A senkrecht verschiebst und ziehe anschließend den Mittelpunkt M nach rechts.

Hinweis: Mit Strg F kannst du die Ansicht wieder auffrischen; dies ist wichtig, wenn du eine neue Spur des Punktes P untersuchen möchtest.

Download der GeoGebra-Datei

1. Erforsche die Bahn des Punktes P bei verschiedenen Kreisradien (verschiebe den Punkt A)!
2. Erforsche die Bahn des Punktes P, wenn er nicht auf dem Kreisumfang, sondern innerhalb des Kreises oder außerhalb liegt (wähle den Radius r mit dem Schieberegler)!
3. Untersuche, wie die Kurve [b t - a sin(t), a - a cos(t)] von der Parametern a und b abhängt (Arbeitsblatt zur Zykloide)!
4. Die Rollkurve ist eine periodische Funktion. Gib diese Periode an und vergleiche mit anderen periodischen Funktionen!

zurück zu Zykloide | zurück zu parametrisierte Kurven