Hochpunkt und Tiefpunkt legen eine symmetrische Polynomfunktion fest
(zu 
- Eigenschaften von Funktionen)
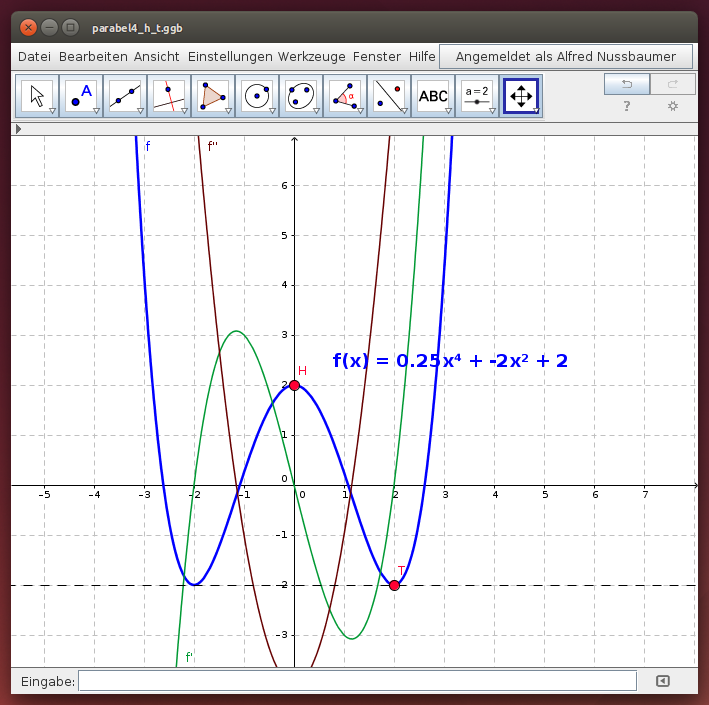
Von einer zur y-Achse symmetrischen Parabel 4. Ordnung sind der Hochpunkt und ein Tiefpunkt gegeben.
Wähle im folgenden GeoGebra-Applet die Positionen der Punkte H,T und lies den Funktionsterm der Parabel 4. Ordnung ab, die durch den Hochpunkt und durch den Tiefpunkt verläuft!
Aufgaben:
- Beschreibe genau, unter welchen Bedingungen die Parabel 4. Ordnung nicht definiert ist!
- Gib die Koordinaten des zweiten Tiefpunkts an!
- Beobachte die 2. Ableitung und gib die Koordinaten der Wendepunkte an!
- Untersuche, wann die Parabel „nach oben“ / „nach unten“ geöffnet ist!
- Bei welcher Lage der Punkte H,T eine Gerade vorliegt!
- Gib das Gleichungssystem an, mit denen die Funktion
aus den Koordinaten der Punkte H, T berechnet werden kann!
Zurück zu Eigenschaften von Funktionen
