Modulo-Inverse
(zu  , Restklassen, Kryptographie)
, Restklassen, Kryptographie)
- Das Einheitselement bezüglich der Multiplikation (mod m) ist 1, denn
(mod m).
- Die Modulo-Inverse r-1 zu r hat die Eigenschaft
(mod m).
Rechenbeispiele:
- Die Modulo-Inverse von 3 (mod 5) ist 2, denn
(mod 5)
- Die Modulo-Inverse von 5 (mod 7) ist 3, denn
(mod 7)
Hinweis: Im letzten Beispiel muss die Gleichung (mod 7) gelöst werden. Da
gilt, ist die Lösung durch Probieren rasch gefunden.
- Gesucht ist die Modulo-Inverse von 4 (mod 8). Also ist die Gleichung
(mod 8) zu lösen. Dies ist nicht möglich, da
eine ungerade Zahl ist und somit kein Vielfaches von 8 sein kann.
Hinweis: In Anwendungen zur Kryptographie (Digitale Unterschrift) wählen wir als Modul eine Primzahl p und bestimmen die Modulo-Inversen zu r (mod p - 1). Dabei setzen wir voraus, dass r und (p - 1) teilferfremd sind.
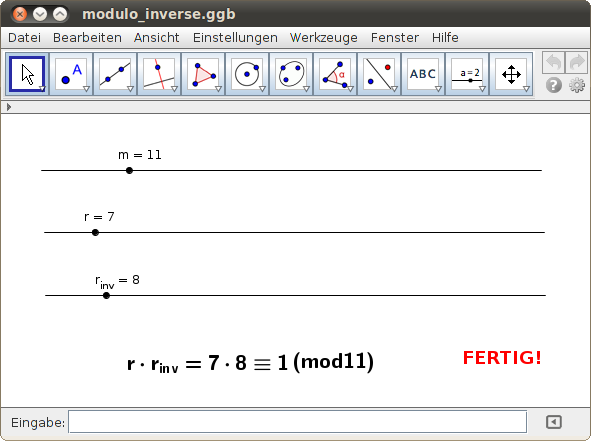
Wähle im folgenden GeoGebra-Beispiel einen Modul m und eine Zahl r. Suche anschließend die Modulo-Inverse rinv!
Aufgaben:
- Achte darauf, dass die Zahlen r und m teilerfremd sind (gcd(r,m) = 1). Untersuche, ob du eine Modulo-Inverse bestimmen kannst, wenn gcd(r,m) = 1 nicht gilt!
- Untersuche: Gibt es immer eine Modulo-Inverse zu r, wenn r und m teilerfremd sind (gcd(r,m) = 1)?
- Ist die Modulo-Inverse eindeutig? Untersuche dies bei verschiedenen Modulen m und vielen Zahlen r!
- Recherchiere: Mit welchen Rechenverfahren kann die Modulo-Inverse bestimt werden?
Zurück zu Restklassen | Kryptographie | Digitale Unterschrift | RSA | GeoGebra 3.2: Texte codieren, Listen bearbeiten, Restklassenarithmetik ...