Inhaltsverzeichnis
Kongruenz und Restklassen
Kongruenz
Wir betrachten die Reste, die bei der Ganzzahldivision auftreten, z.B.:
12 : 7 = 1, 5 R 24 : 5 = 4, 4 R ...
Wir sagen:
(mod 7)
(mod 5)
…
Da
24 : 5 = 4, 4 R 9 : 5 = 1, 4 R
gilt, und da offensichtlich die Zahl 24 als auch die Zahl 9 bei der Division durch die gleiche Zahl 5 den gleichen Rest 4 liefern, heißen die beiden Zahlen 24 und 9 (und unendlich viele weitere) kongruent bezüglich des Moduls 5:
(mod 5)
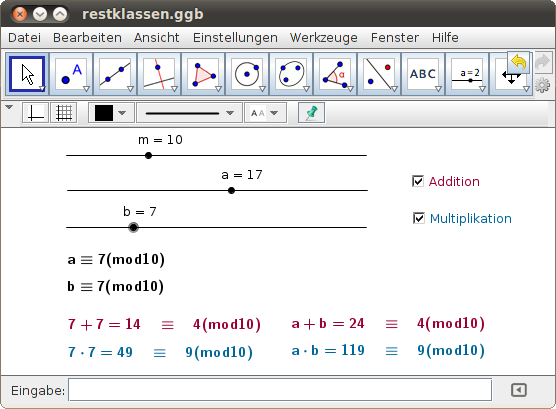
Rechenregeln für Kongruenzen
Für ganze Zahlen , a, b, c,
(mod m), d,
(mod m), k, gelten folgende Rechenregeln:
(mod m)
(mod m)
(mod m)
Überprüfe im folgenden GeoGebra-Beispiel die Rechengesetze für die Addition und Multiplikation (mod m):
Zyklische Gruppen
Zyklische Gruppen bestehen aus allen Potenzen eines einzelnen Elements g. g heißt das erzeugende Element.
Wir betrachten besondere Restklassengruppen, nämlich solche, deren Modul m eine Primzahl p ist.
Beispiele für zyklische Gruppen
Z7 = {0,1,2,3,4,5,6}, Z7* = {1,2,3,4,5,6}
Z11 = {0,1,2,3,4,5,6,7,8,9,10}, Z11* = {1,2,3,4,5,6,7,8,9,10}
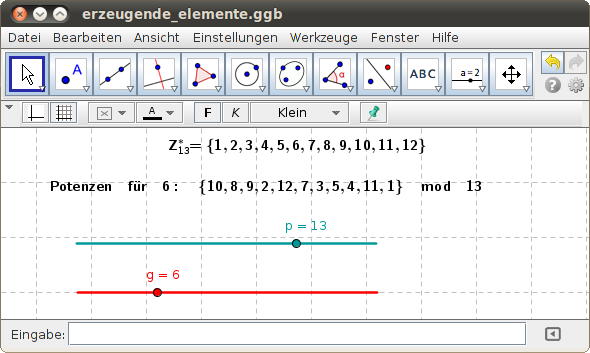
Eine zyklische Gruppe Zp, p eine Primzahl, hat p - 1 Elemente; ihre erzeugenden Elemente heißen Primitivwurzeln
Beispiel: Erzeugendes Element, Primitivwurzel
2 ist kein erzeugendes Element von Z7*:
,
,
,
,
mod 7
3 ist ein erzeugendes Element von Z7:
,
,
,
mod 7
Eine zyklische Gruppe kann mehrere verschiedene erzeugende Elemente haben, z.B. ist auch 5 ein erzeugendes Element für Z7*
Aufgaben:
Suche erzeugende Elemente für zyklische Gruppen bis p = 17 mit dem folgenden GeoGebra-Beispiel. Wähle zunächst die Primzahl p und teste anschließend für verschiedene Elemente g, ob sie Primitivwurzeln sind!
- Gib alle erzeugenden Elemente für eine gewählte zyklische Gruppe an!
- Sobald sich ein Ergebnis in der Potenzreihe wiederholt, kann g kein erzeugendes Element sein. Begründe!
Zurück zu Lernpfad Kryptographie | GeoGebra 3.2: Texte codieren, Listen bearbeiten, Restklassenarithmetik ...