(zu , Kryptographie)

Der RSA-Algorithmus wurde 1977 von Ron Rivest, Adi Shamir und Leonard Adleman entwickelt. Das Verfahren verwendet große Primzahlen - seine Sicherheit basiert auf der Schwierigkeit, große Zahlen zu faktorisieren. Der Algorithmus ist einfach zu verstehen und ebenso leicht in Applikationen zu implementieren. Es hat sich als asymmetrisches Verschlüsselungsverfahren für zahlreiche Anwendungen etabliert:

• Wähle zufällig und stochastisch unabhängig zwei verschiedene Primzahlen p und q, die etwa gleich lang sein sollen und berechne das Produkt .
• Berechne , wobei Φ für die eulersche Φ-Funktion steht.
• Wähle eine Zahl 1 < e < Φ(N), die teilerfremd zu Φ(N) ist.
• Berechne die Zahl d so, dass (mod Φ(N)) gilt. Der öffentliche Schlüssel besteht dann aus N (dem Primzahlenprodukt) und e (dem öffentlichen Exponenten).
• Der private Schlüssel besteht aus N (dem öffentlich bekannten Primzahlenprodukt) d (dem privaten Exponenten).

Hinweis: p, q und Φ(N) werden nicht weiter benötigt und sollten nach der Erzeugung des Schlüssels auf sichere Weise gelöscht werden.

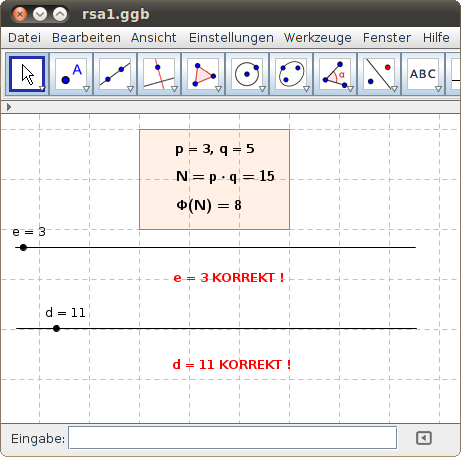
Wir wählen die (kleinen) Primzahlen p = 3 und q = 5, also gilt N = 15.

Im nächsten Schritt suchen wir eine Zahl e, die kleiner als N, aber keine gemeinsamen Teiler mit Φ(N) hat:

Φ(N) = (p - 1) (q - 1) = 2 · 4 = 8

e muss also eine ungerade Zahl sein, wir wählen den kleinen Wert e = 3.

Nun suchen wir die Modulo-Inverse d (mod 8), es muss gelten (mod 8). Dies können wir durch Probieren oder durch das Lösen der diophantischen Gleichung

erreichen. In unserem einfachen Fall kann x = 4 gewählt werden, dann ist d = 11.

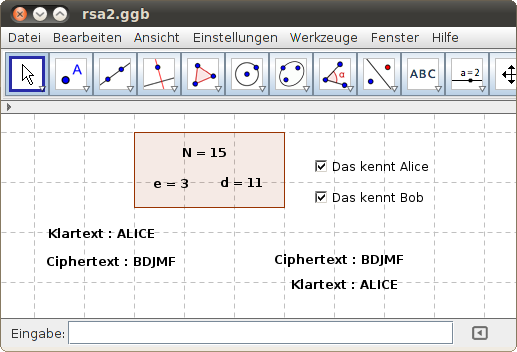
Wir haben also p = 3, q = 5, N = 15, d = 11 und e = 3. Somit stehen uns der Private Key (15, 11) und der Public Key (15, 3) zur Verfügung. Die Größen p, q, Φ(N) = (p - 1)(q-1) und x werden nicht mehr benötigt und sollten gelöscht werden.

Im ersten Schritt bestimmen wir den öffentlichen Schlüssel (N,e) und den privaten Schlüssel (N, d). Gib dazu die gewünschten Werte für die Primzahlen p und q über die Eingabezeile ein, suche mit dem Schieberegler einen gültigen Wert für e und anschließend eine passende Modulo-Inverse d:

Download der GeoGebra-Datei

Übertrage die gefunden Werte in das folgende GeoGebra-Beispiel und wähle einen geeigneten Klartext, den du der Variablen „Klartext“ in der Eingabezeile zuweist:

Download der GeoGebra-Datei

• Die Zahlen für p und q müssen klein bleiben, damit die Potenzen im Algorithmen noch definiert sind. Warum ist diese Beschränkung jedenfalls problematisch?
• Nur Buchstaben, deren Indizes kleiner als N sind, können korrekt verschlüsselt bzw. entschlüsselt werden. Teste dies für eine bestimmte Wahl von N, indem du den Klartext „ABCDEFGH….“ eingibst!
• Realisiere den RSA-Algorithmus mit einem CAS und teste seine Eigenschaften!

Zurück zu Lernpfad Kryptographie | GeoGebra 3.2: Texte codieren, Listen bearbeiten, Restklassenarithmetik ...