Lineares Wachstumgsmodell
Ein lineares Wachstum liegt vor, wenn die (relative) Änderungsrate (der Zuwachs pro Zeitschritt) konstant ist.
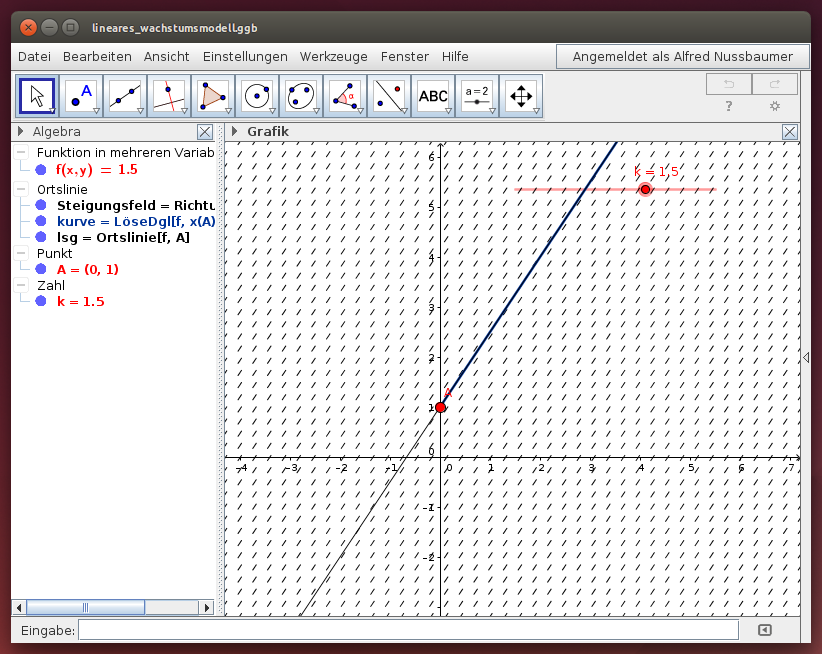
Im folgenden GeoGebra-Beispiel wird die Lösung der Differentialgleichung dargestellt:
Aufgaben:
- Variiere k und erkläre, wie die Lösung der Differentialgleichung
von k abhängt!
- Variiere den Anfangswert A und beschreibe, wie die Bestandsgröße y vom Anfangswert A abhängt!
- Stelle Richtungsfeld und die Lösungsfunktion durch den Anfangswert A für verschiedene Werte des Parameters k in Differentialgleichung
dar! Gib mögliche Wachstumsprozesse an!
- Interpretiere einen Wachstumsprozess mit
!
- Modelliere einen analogen diskreten Wachstumsprozess (z.B. mit Hilfe der Tabellenkalkulation)!
Zurück zu Dynamische Systeme
Weiter zu Langzeitverhalten der linearen Differenzengleichung
Weiter zu Exponentielles Wachstumsmodell | Beschränktes Wachstumsmodell | Logistisches Wachstumsmodell | AN1.1 | AN1.2