Inhaltsverzeichnis
Dynamische Systeme
Diskrete Modelle - Differenzengleichungen
Diskrete Wachstumsmodelle werden mit rekursiven Folgen beschrieben. Wir berechnen alle Folgenglieder durch Iteration in der Tabellenansicht.
Beispiel: Abkühlkurve (beschränktes Wachstum)
(vgl. Beschränktes Wachstumsmodell)
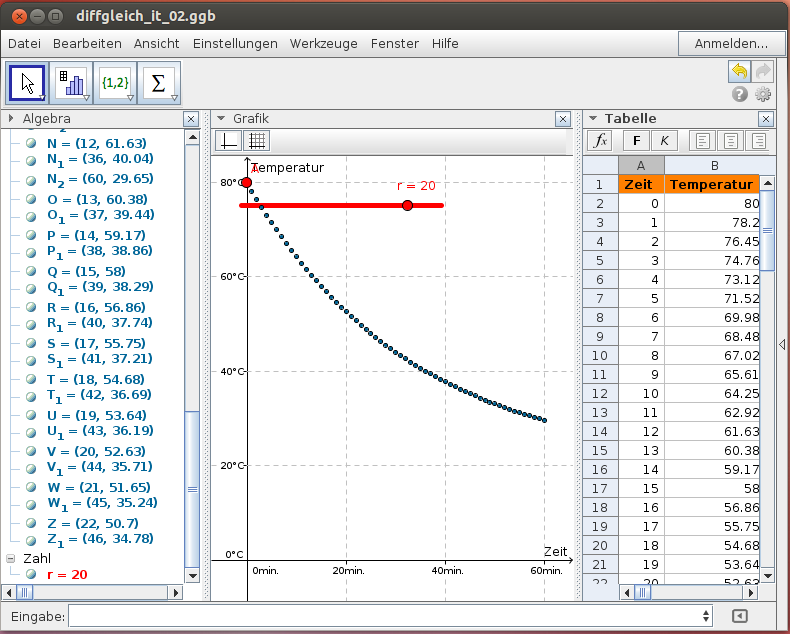
80°C heißes Wasser kühlt bei einer Raumtemperatur von 20°C während eines Zeitraumes von 60 Minuten ab. Bestimme die Abkühlkurve!
mit
Wir erhalten aus obiger Iterationsgleichung die folgende Differenzengleichung:
mit
,
mit
Beispiel: Bewegung im Kraftfeld eines Zentralkörpers
Differenzengleichungen sind - etwa bei zweidimensionalen Modellen zur Bewegung eines Körpers in einem Kraftfeld - auch für Vektoren möglich. So wird etwa die Position eines Körpers nach einem Zeitschritt
aus seiner (momentanen) Geschwindigkeit
mit einer Differenzengleichung für Vektoren berechnet:
Solche iterativen Berechnungen mit Vektoren sind natürlich eine hübsche Anwendung in der Tabellenansicht!
Beispiel: Fischpopulation (logistisches Wachstum)
(vgl. Logistisches Modell)
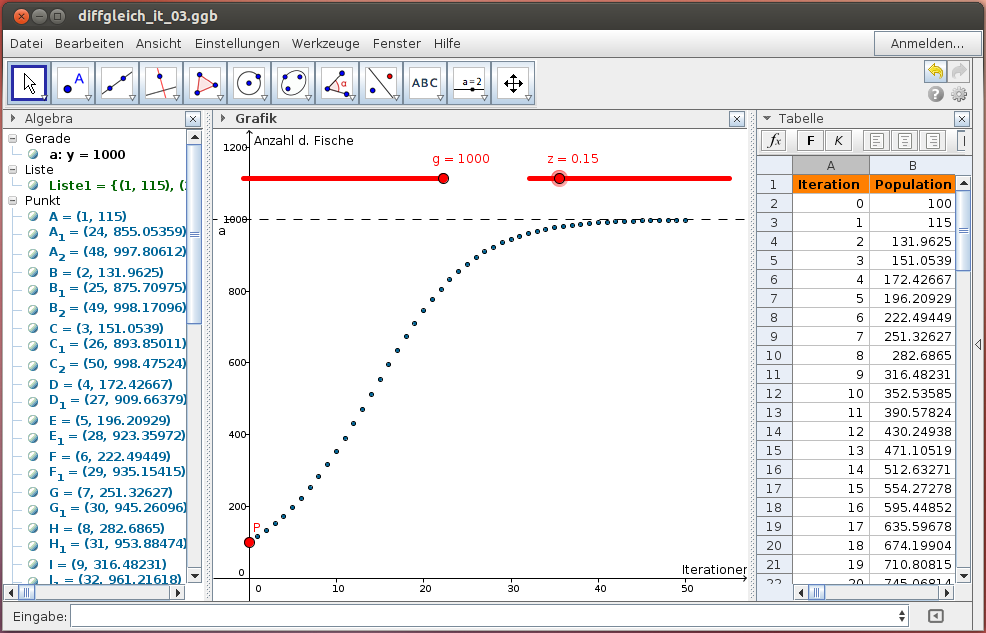
Zu Beginn sind es 100 Fische, im ersten Jahr kommt es zu einem Zuwachs von 15 %. Der Lebensraum ist auf 1000 Fische beschränkt. Beschreibe die Entwicklung der Fischpopulation durch ein logistisches Modell!
Kontinuierliche Modelle - Differentialgleichungen
Beispiel: Abkühlkurve (beschränktes Wachstum)
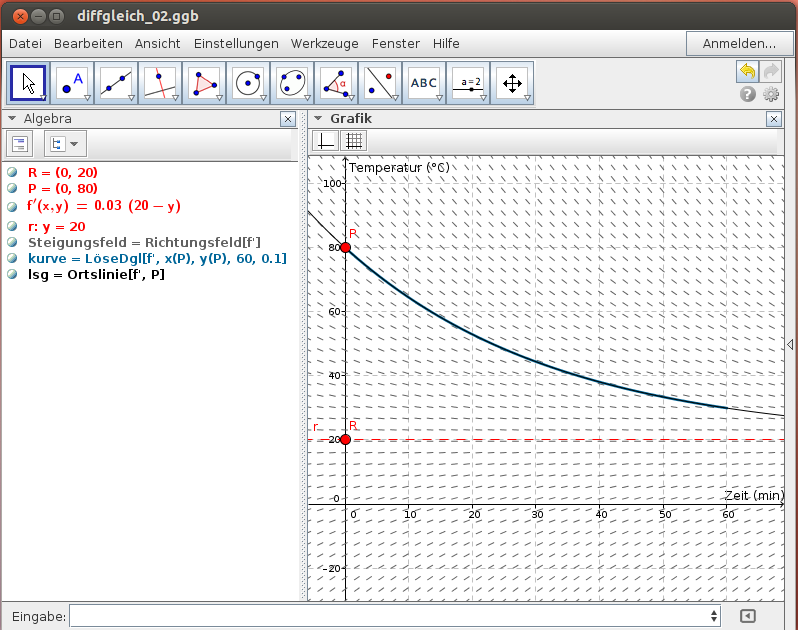
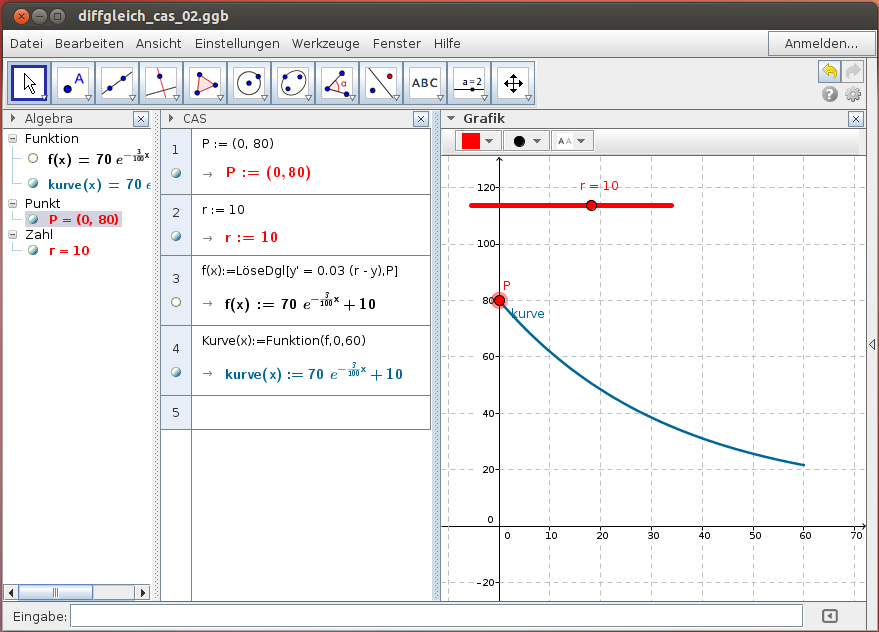
80°C heißes Wasser kühlt bei einer Raumtemperatur von 20°C während eines Zeitraumes von 60 Minuten ab. Bestimme die Abkühlkurve!
Die Differenzengleichung gibt die Änderung der Zustandsgröße abhängig von einem diskreten Zeitschritt an. Durch Grenzwertbildung
erhalten wir die Differentialgleichung:
mit
Wir lösen die Differentialgleichung entweder numerisch in der Algebra-Ansicht oder exakt in der CAS-Ansicht.
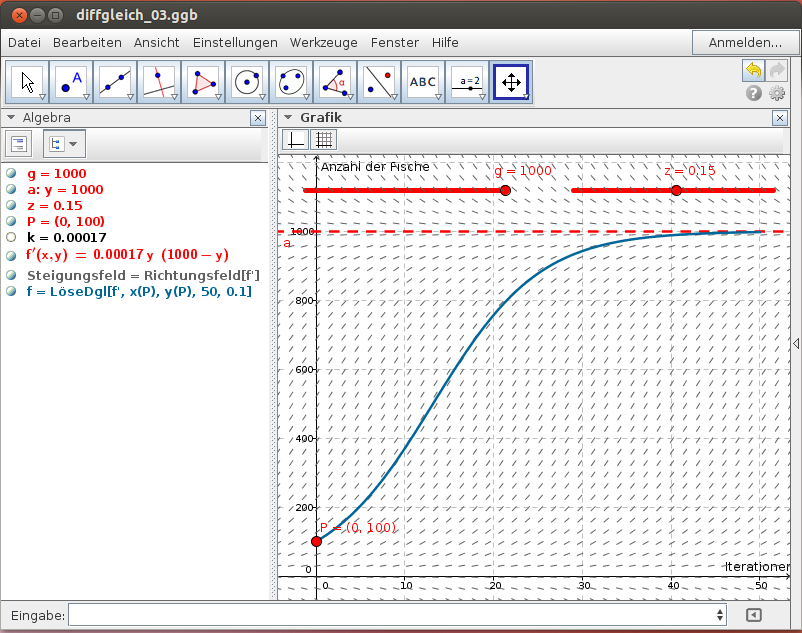
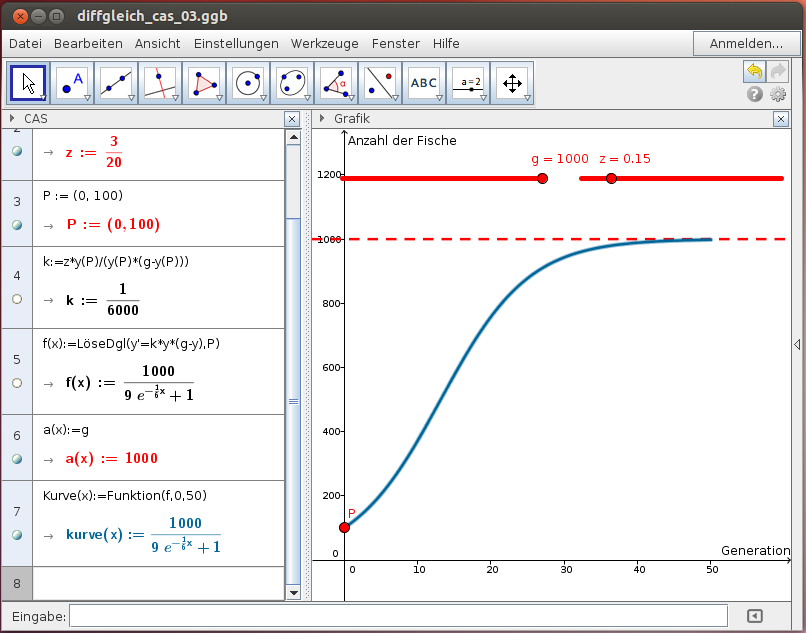
Beispiel: Fischpopulation (logistisches Wachstum)
Zu Beginn sind es 100 Fische, im ersten Jahr kommt es zu einem Zuwachs von 15 %. Der Lebensraum ist auf 1000 Fische beschränkt. Beschreibe die Entwicklung der Fischpopulation durch ein logistisches Modell!
Numerische Lösung (Algebra-Ansicht):
Zurück zu Themenheft Arbeiten mit GeoGebra 7 - 8