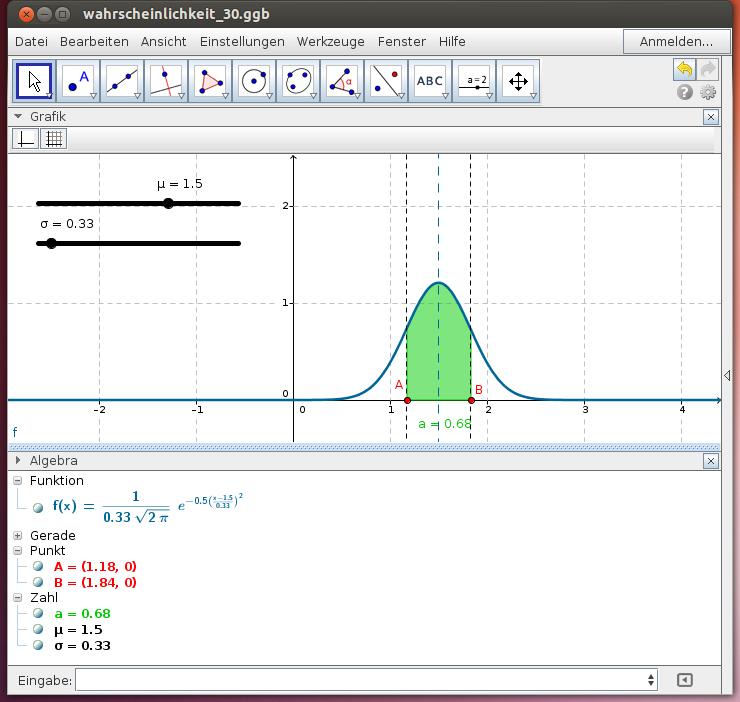
Die Eigenschaften der Gauß'schen Glockenkurve
8, S. 82 - 83
Die Funktion ![tex:f(x) = \frac 1 {\sigma \cdot \sqrt{2 \pi}} \cdot e^{-\frac 1 2 \left( \frac {x-\mu} \sigma \right)^2]()
heißt Gauß'sche Glockenkurve mit den Parametern ![tex:\mu]()
und ![tex:\sigma]()
.
Die Gauß'sche Glockenkurve approximiert die Streifen der Binomialverteilung im Allgemeinen gut.
Aufgaben:
- Wähle verschiedene Werte für μ und beschreibe die Auswirkung auf die Gauß'sche Glockenkurve!
- Wähle verschiedene Werte für σ und beschreibe die Auswirkung auf die Gauß'sche Glockenkurve!
- Wähle die linke und die rechte Grenze für die Fläche unterhalb der Kurve und lies den Flächeninhalt a ab!
- Ordne die senkrechten Geraden den Werten für μ, μ - σ und μ + σ zu und berechne den Inhalt der Fläche unter der Kurve zwischen μ - σ und μ + σ!
- Bestimme den Inhalt der Fläche unter der Gauß'schen Glockenkurve über einen „großen Bereich“ und interpretiere das Ergebnis!
- Stelle die 1. Ableitung der Gauß'schen Glockenkurve dar und lies Eigenschaften der Gauß'schen Glockenkurve ab!
- Stelle die 2. Ableitung der Gauß'schen Glockenkurve dar und lies Eigenschaften der Gauß'schen Glockenkurve ab!
Zurück zu Stochastik | WS3.4
