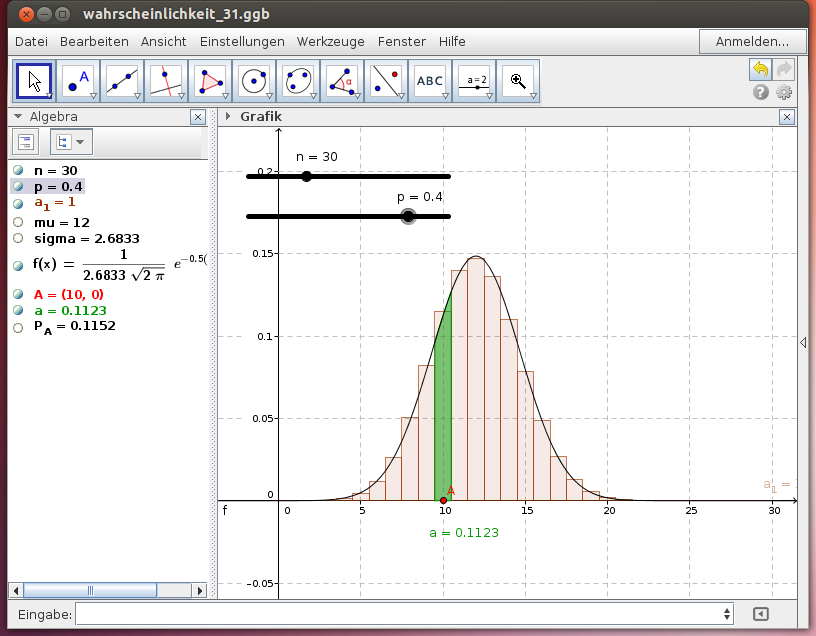
Stetigkeitskorrektur
Die Gauß'sche Glockenkurve nähert die Binomialverteilung gut an. Zur Berechnung der Wahrscheinlichkeit P(X = a) (1 Streifen) verwenden wir das Integral unter der Glockenkurve im Intervall [a - 0,5; a + 0.5].
Begründe dies anhand des folgenden GeoGebra-Beispiels!
Aufgaben:
- Wähle verschiedene Werte für n, p und a = x(A) und interpretiere die Werte für P(X=a) und für das bestimmte Integral über dem Intervall [a - 0.5; a + 0.5]!
- Begründe, warum die Stetigkeitskorrektur für wenige Streifen der Binomialverteilung angewendet wird, und warum sie bei vielen (dünnen) Streifen wegbleiben kann!
Zurück zu Stochastik | WS3.4