Das Orthogonalitätskriterium
5, S. 190, BIFIE GK AG3.3
Zwei Vektoren ![tex:\vec a]()
und ![tex:}\vec b]()
sind orthogonal, wenn sie einen rechten Winkel einschließen.
Das skalare Produkt von Vektoren ist genau dann null, wenn sie orthogonal sind:
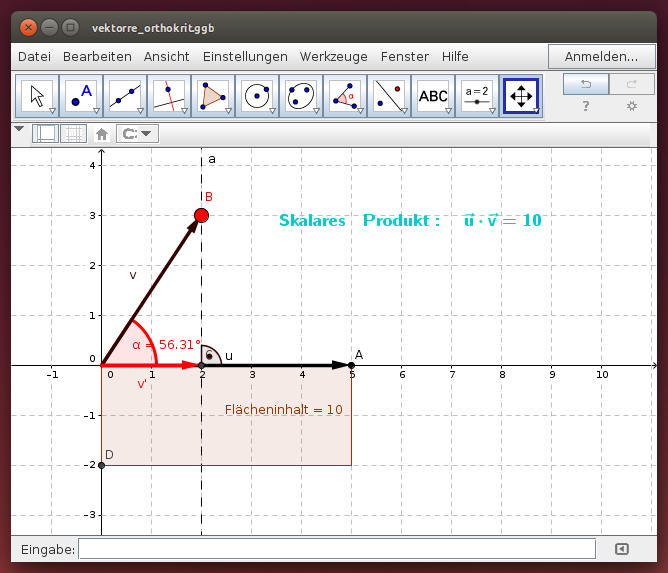
Begründe das Orthogonalitätskriterium anhand der geometrischen Interpretation des skalaren Produkts. Variiere die Lage des Vektors v, indem du den roten Punkt B verschiebst:
Aufgaben:
- Lege im obigen GeoGebra-Beispiel Normalvektoren zum gegebenen Vektor fest!
- Beurteile und begründe: Zu einem gegebenen Vektor ist der Normalvektor nicht eindeutig …
Ausblick: Rechnen mit Vektoren im Raum
Zurück zu Vektorrechnung
