Inhaltsverzeichnis
Lernpfad: Vierecke
(zu 
5 S. 220 -222, 7)
Du fasst in diesem Lernpfad das Wissen aus der „Elementargeometrie“ der Unterstufe zusammen, erweiterst es um neue Aspekte, Begründungen und Beweisen und stellst dein Wissen in Zusammenhang mit Objekten der nichtlinearen analytischen Geometrie (Kreis, Ellipse, Parabel, Hyperbel).
Die Familie der Vierecke
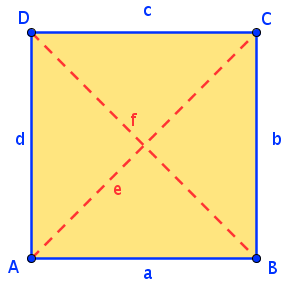
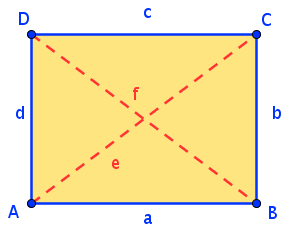
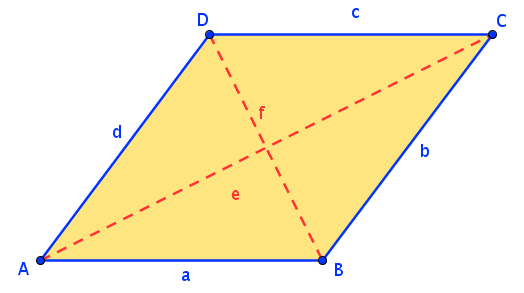
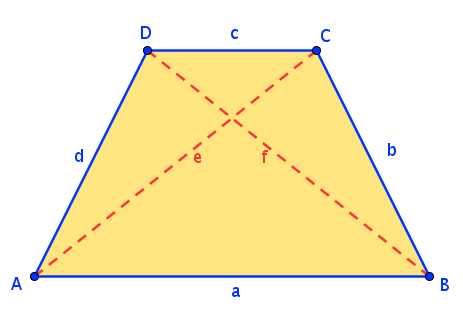
Fasse - ausgehend vom Quadrat - alle Vierecke zusammen und gib an, welches Viereck welche Eigenschaften eines anderen Vierecks hat!
 Quadrat | ||
 Rechteck |  Raute |
|
 Gleichschenkliges Trapez |  Parallelogramm |  Deltoid |
 Trapez als Sehnenviereck | ||
 Sehnenviereck |  Trapez |  Deltoid als Tangentenviereck |
 Tangentenviereck |
||
 Viereck |
Sonderformen
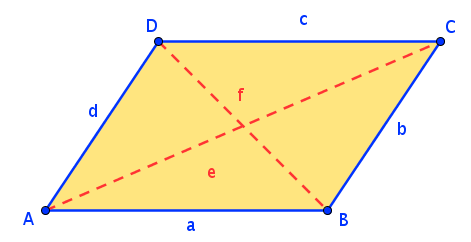
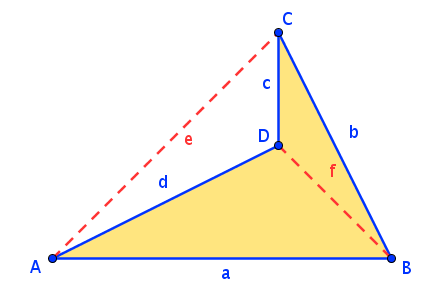
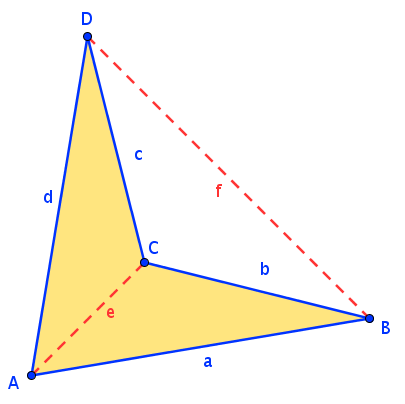
Im konvexen Viereck liegen die Diagonalen innerhalb des Vierecks. Bei Vierecken mit „einspringenden Ecken“ (konkave Vierecke) liegt eine Diagonale außerhalb des Vierecks:
Einen Sonderfall stellt das konkave Deltoid dar:
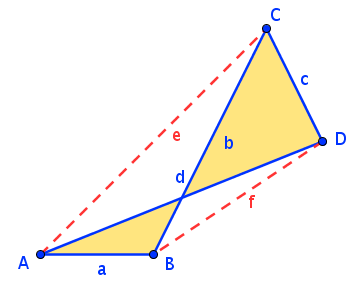
Beim überschlagenen Viereck liegen beide Diagonalen außerhalb des Vierecks - zwei Seiten schneiden einander.
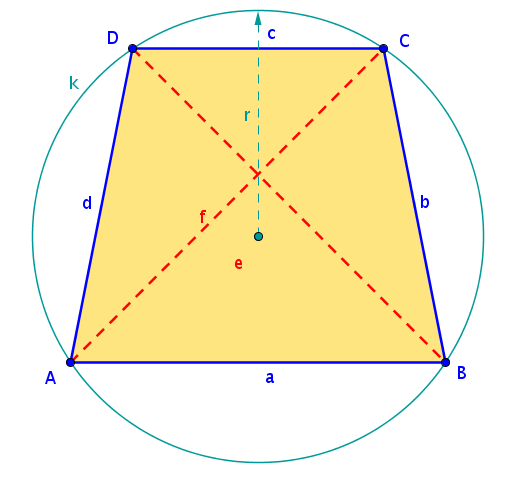
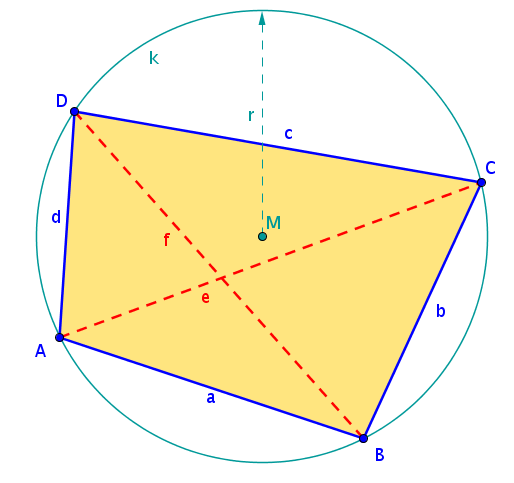
Sehnenviereck
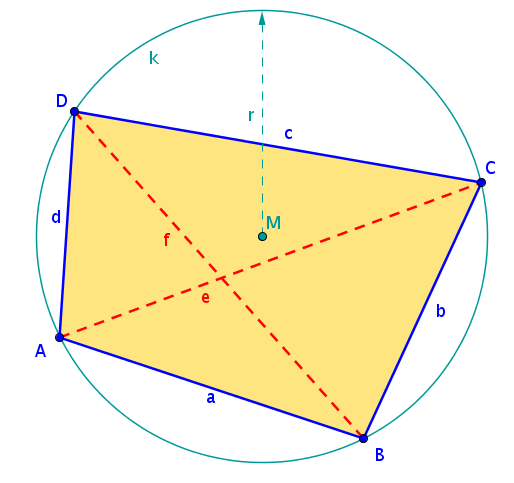
Beim Sehnenviereck liegen alle vier Eckpunkte auf einem Kreis, das Sehnenviereck hat somit einen Umkreis.
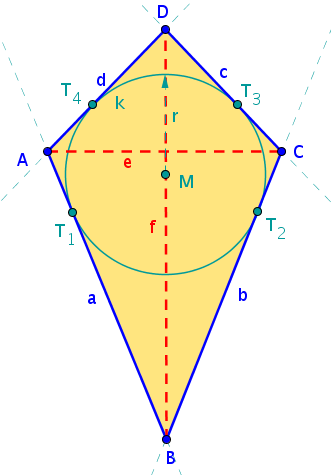
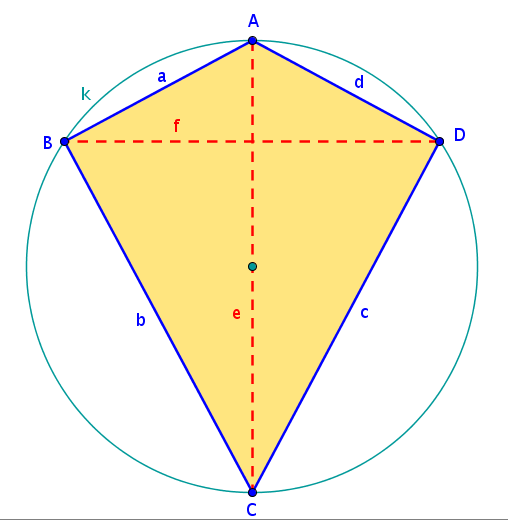
Einen interessanten Spezialfall kannst du beim Deltoid betrachten, das zugleich ein Sehnenviereck ist. Gib seine besonderen Eigenschaften an:
Lies Details im Artikel zum Sehnenviereck nach und löse die dort gestellten Aufgaben!
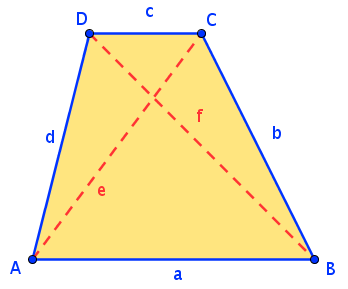
Tangentenviereck
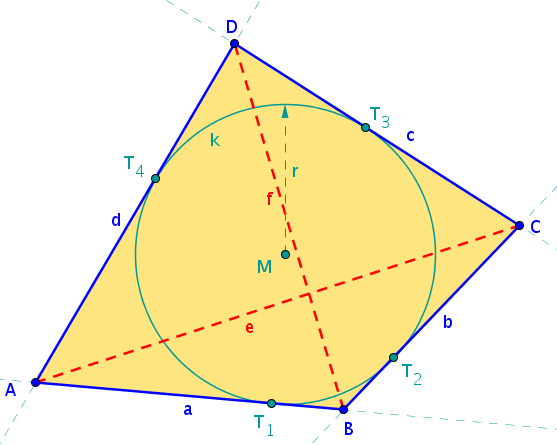
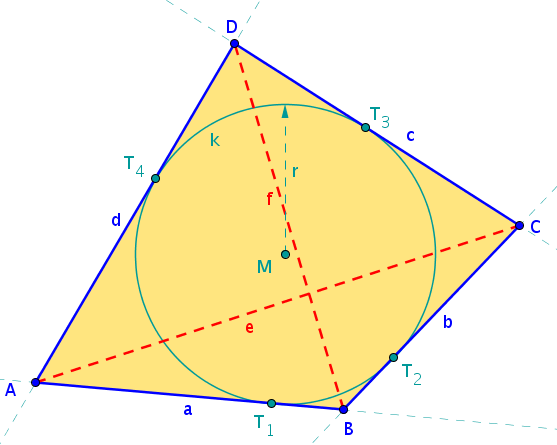
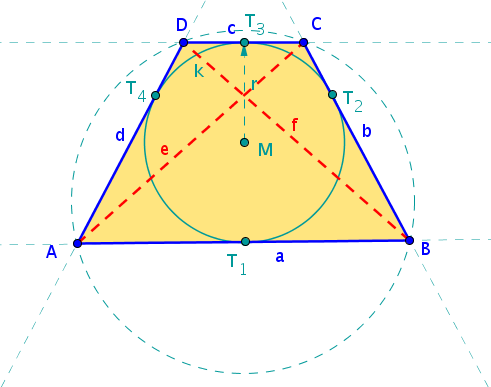
Beim Tangentenviereck berühren alle Seiten des Vierecks einen Kreis, das Tangentenviereck hat somit einen Inkreis.
Einen interessanten Spezialfall kannst du beim Trapez betrachten, das zugleich ein Tangentenviereck ist. Gib seine besonderen Eigenschaften an:
Lies Details im Artikel zum Tangentenviereck nach und löse die dort gestellten Aufgaben!
Eingeschriebene Vierecke
In einen Kreis, in einer Ellipse oder Halbellipse können Vierecke eingeschrieben sein - oft sind sie symmetrisch. Skizziere solche Kurven und Vierecke und fasse ihre Eigenschaften zusammen!
Flächenberechnung
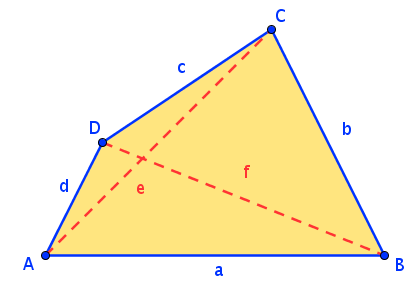
Jedes Viereck kann aus zwei Dreiecken zusammengesetzt werden: Erkläre, wie daher der Flächeninhalt eines jeden Viereckes bestimmt werden kann!
Eräutere und begründe die folgenden Formeln für den Flächeninhalt:
- Diagonalen e und f stehen aufeinander normal:
- Im allgemeinen Viereck gilt:
- Erläre, wie die Formel für den Flächeninhalt eines Vierecks mit aufeinander normal stehenden Diagonalen aus der Flächeninhaltsformel für das allgemeine Viereck folgt!
Zurück zu Lernpfade
