Zurück zu: 5.Klasse » Analytische Geometrie der Ebene

Sehnenviereck

(zu Thema Mathematik 5 5, S. 220 - 222)

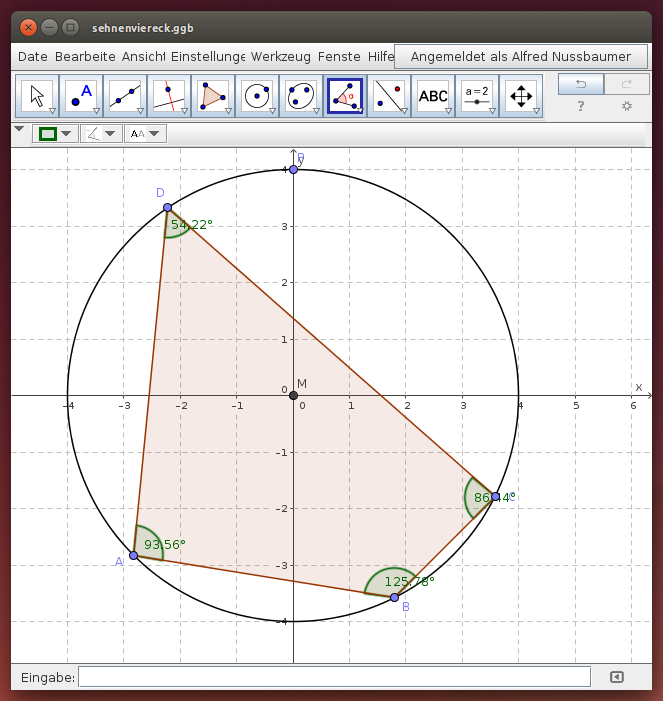
Ein Sehnenviereck ist ein Viereck, dessen Eckpunkte auf einem Kreis liegen. Die Seiten sind somit Sehnen des Kreises.

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Aufgaben:

  • Überprüfe, dass gegenüberliegende Winkel des Sehnenvierecks supplementär sind: tex:\alpha + \gamma = 180^\circ, tex:\beta + \delta = 180^\circ (Hinweis: Zeichne die entsprechenden Winkel im GeoGebra-Beispiel ein und gib ihre Größen an)!
  • Beweise den Satz (Hinweis: Verwende den Peripheriewinkelsatz)!

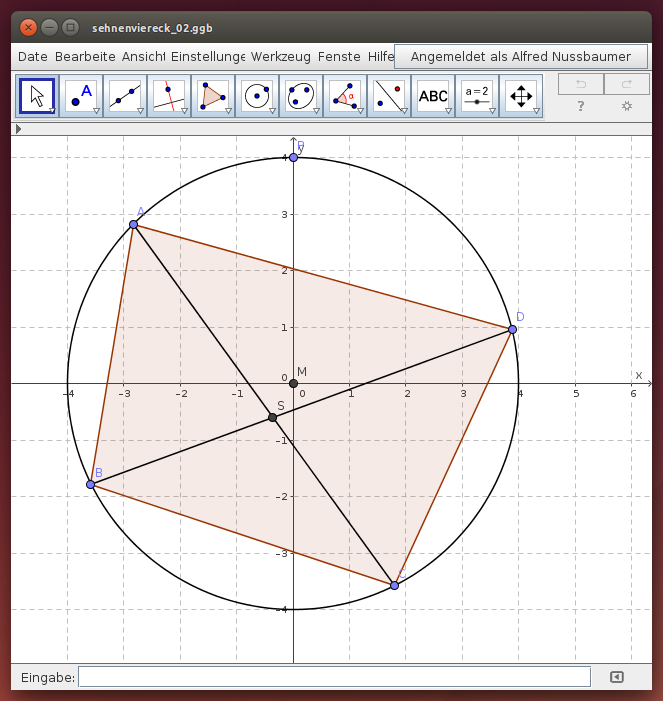
Untersuche weitere Eigenschaften im folgenden GeoGebra - Beispiel. Sie beziehen sich auf die Seitenlängen a, b, c und d des Vierecks, auf die Längen der Diagonalen e und f sowie auf die Abschnitte der Diagonalen von den Eckpunkten zu ihrem Schnittpunkt S.

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

  • tex:\overline {AS} \cdot \overline{CS} = \overline{BS} \cdot \overline{DS} („Sehnensatz“)
  • tex:e = \sqrt{\frac{(ac+bd)(ad+bc)}{ab+cd}}
  • tex:f = \sqrt{\frac{(ab+cd)(ac+bd)}{ad+bc}}
  • tex:a \cdot c + b \cdot d = e \cdot f
  • Für den Flächeninhalt A des Vierecks gilt: tex:A = \frac{e \cdot (ab + cd)}{4R} = \frac{f \cdot (ad + bc)}{4R} (R … Kreisradius)
  • Für den Radius R gilt: tex:R = \frac 1 {4A} \cdot \sqrt{(ab+cd)(ac+bd)(ad+bc)} (A … Flächeninhalt des Vierecks)

Zurück zu Analytische Geometrie der Ebene


Zuletzt angesehen: • sehnenviereck