Untersumme und Stammfunktion
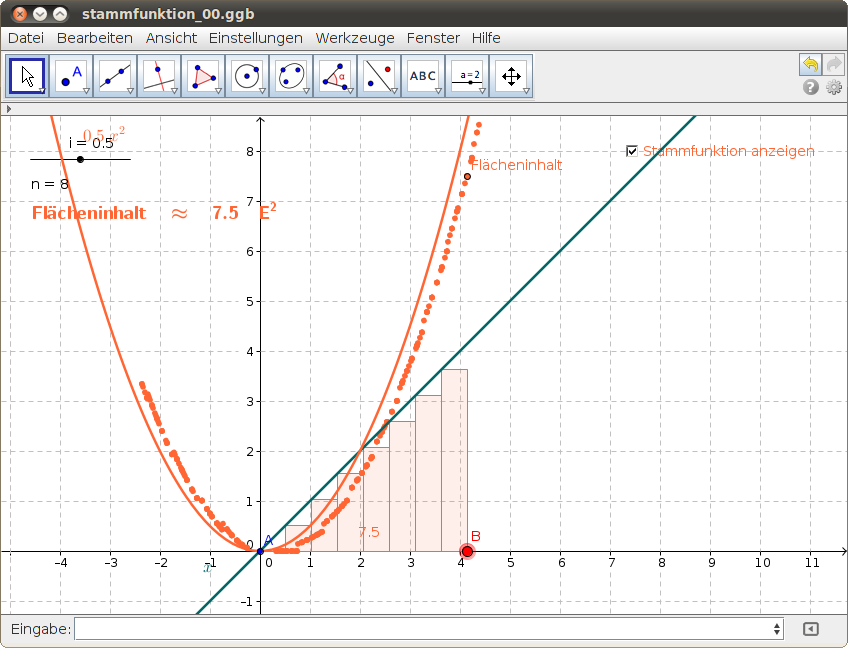
Wir berechnen den Flächeninhalt unter einer Kurve näherungsweise, indem wir die Fläche unter der Kurve im Intervall [A,B] mit gleich breiten Rechteckstreifen auslegen. Diese Rechteckstreifen reichen nicht über den Funktionsgraph hinaus - sie bilden eine Untersumme.
Wähle im folgenden GeoGebra-Beispiel die Breite der Rechteckstreifen mit der Variablen i und verschiebe die rechte Grenze B des Intervalls. Beobachte, wie der (näherungsweise) berechnete Flächeninhalt von der rechten Intervallgrenze B abhängt:
Aufgaben:
- Begründe, warum die Punktespur für den Flächeninhalt „stufig“ verläuft!
- Variiere die Breite i der Rechteckstreifen und interpretiere die Ergebnisse für die Flächeninhalte!
- Verschiebst du B in den negativen Bereich des Zahlenachse, so reichen die Rechteckstreifen über den Funktionsgraph hinaus. Es liegt eine Obersumme vor. Was beobachtest Du für die Flächeninhalte und für die Punktespur?
- Stelle die Stammfunktion der Funktion f(x) mit Hilfe des Kontrollkästchens dar und vergleiche mit der Punktespur der Flächeninhalte!
- Gib andere Potenzfunktionen oder die Quadratwurzelfunktion für f(x) in der Eingabezeile ein und beobachte wie oben!
- Welche Ergebnisse erhältst du für die Sinus- oder Kosinusfunktion? Was fällt dir für die e-Funktion auf? Experimentiere mit der natürlichen Logarithmusfunktion und interpretiere die Ergebnisse!
Zurück zu Lernpfad Bestimmtes Integral | AN4.1