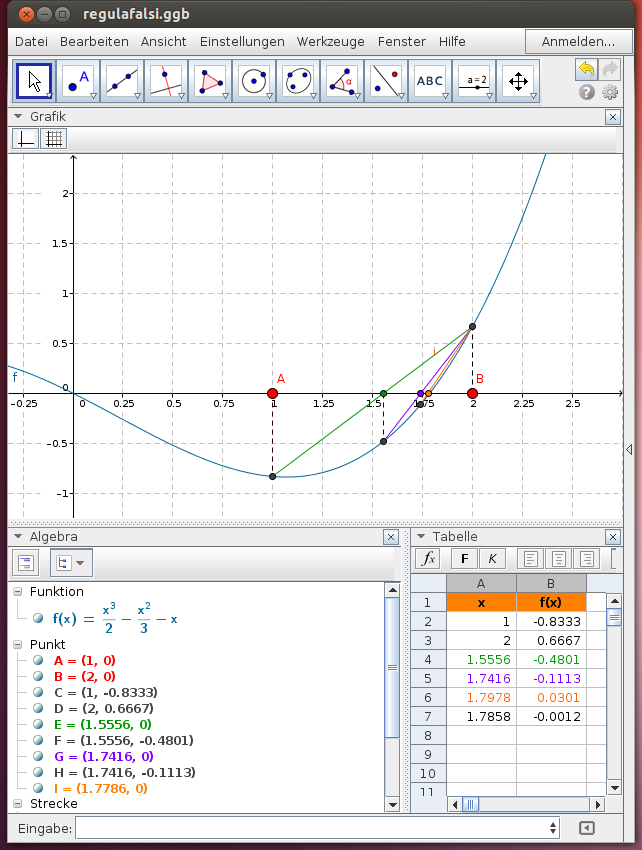
Die Regula Falsi

tm.jpg 6, S. 42 - 43

Bei diesem Näherungsverfahren wird die Lösung der Gleichung tex:f(x) = 0 näherungsweise aus zwei Startwerten berechnet, die „links“ und „rechts“ von der erwarteten Nullstelle liegen.

  1. Suche zwei Startpunkte, die nahe „links“ und „rechts“ von der erwarteten Nullstelle liegen.
  2. Suche die zugehörigen Funktionswerte auf dem Funktionsgraphen.
  3. Verbinde diese beiden Punkte und schneide diese Strecke mit der x-Achse.
  4. Dieser Schnittpunkt liegt näher zur Nullstelle als die beiden Startwerte.

Im folgenden Beispiel wird der dritte Schnittpunkt der Funktion tex:f(x) = \frac {x^3} 2 - \frac {x^2} 2 - x aus den beiden Startwerten tex:x_1=1 (Punkt A) und tex:x_2 = 2 (Punkt B) bestimmt.

Es gilt: tex:x_{neu} = x_1 - f(x_1) \cdot \frac {x_1 - x_2} {f(x_1) - f(x_2)}.

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Beachte: Die näherungsweise Berechnung erfolgt schrittweise durch Iteration. Es ist somit günstig, diese Berechnungsschritte in der Tabellenansicht auszuführen.

Aufgaben:

  • Begründe die Berechnungsformel A4 = A2 - B2 (A2 - A3)/(B2 - B3)!
  • Variiere die Startwerte, indem du die Punkte A und B verschiebst und beobachte die Konstruktion der ersten Näherungswerte!
  • Vergleiche mit dem Bisektionsverfahren!
  • Vergleiche mit dem newtonschen Näherungsverfahren!

Zurück zu Gleichungen und Ungleichungen | Folgen und Reihen


Zuletzt angesehen: • regula_falsi