Inhaltsverzeichnis
Nullstellen näherungsweise bestimmen
 6, S. 42 - 43, 7, S. 208 - 209
6, S. 42 - 43, 7, S. 208 - 209
Das Auffinden einer Nullstelle der Funktion entspricht dem Lösen der Gleichung
. Wir besprechen somit Methoden, um Gleichungen der Form
näherungsweise zu lösen.
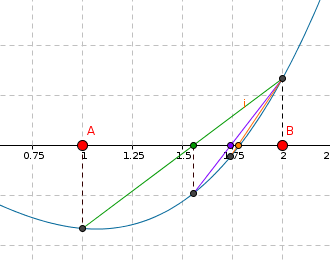
Die Regula Falsi
Ausgehend von zwei Startwerten „links“ und
„rechts“ von der Nullstelle bestimmen wir den nächsten Näherung
mit der folgenden Formel:
Geometrisch entspricht dies dem Schnittpunkt der Strecke zwischen den beiden zu und
gehörenden Punkten auf dem Funktionsgraph mit der x-Achse.
Aufgaben:
- Wende die Regula Falsi auf selbst gewählte Beispiele an und löse das Näherungsverfahren a) geometrisch in der Grafikansicht, b) iterativ in der Tabellenansicht!
- Lies zur geschichtlichen Entwicklung nach!
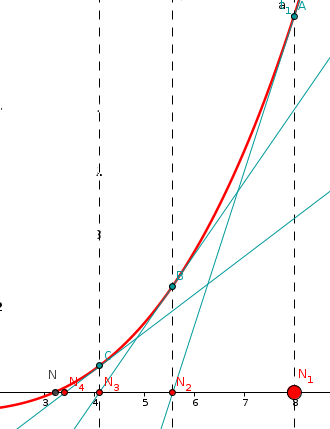
Das newtonsche Näherungsverfahren
Ausgehend von einem Startwert „in der Nähe“ der Nullstelle bestimmen wir die nächste Näherung
mit der folgenden Formel:
Geometrische entspricht dies dem Schnittpunkt der Tangente an den Funktionsgraph in dem zu gehördenen Punkt auf dem Funktionsgraph mit der x-Achse.
Aufgaben:
- Wende das newtonsche Näherungsverfahren auf selbst gewählte Beispiele an und löse das Näherungsverfahren a) geometrisch in der Grafikansicht, b) iterativ in der Tabellenansicht!
- Lies zur geschichtlichen Entwicklung nach!
Zurück zu Gleichungen und Ungleichungen | Bisektionsverfahren | Regula Falsi | newtonsches Näherungsverfahren