(zu 7)

Bereits in der 5. Klasse ( 5, S. 95) haben wir ein Näherungsverfahren besprochen, mit dem die Lösungen der quadratischen Gleichung x² + px + q = 0 näherungsweise gefunden werden können, "wenn die Wurzeltaste am Taschenrechner klemmt". Führe das zugehörige GeoGebra-Beispiel schrittweise aus und wiederhole die Berechnungs- und Konstruktionsschritte!

1. Beginne mit einem Startwert „in der Nähe der Nullstelle“.
2. Bestimme den zu diesem Startwert gehörenden Punkt auf dem Funktionsgraphen.
3. Bestimme für diesen Punkt die Tangente an den Funktionsgraphen.
4. Schneide die Tangente mit der x-Achse: Dieser Schnittpunkt liegt näher zur Nullstelle als der Startwert …

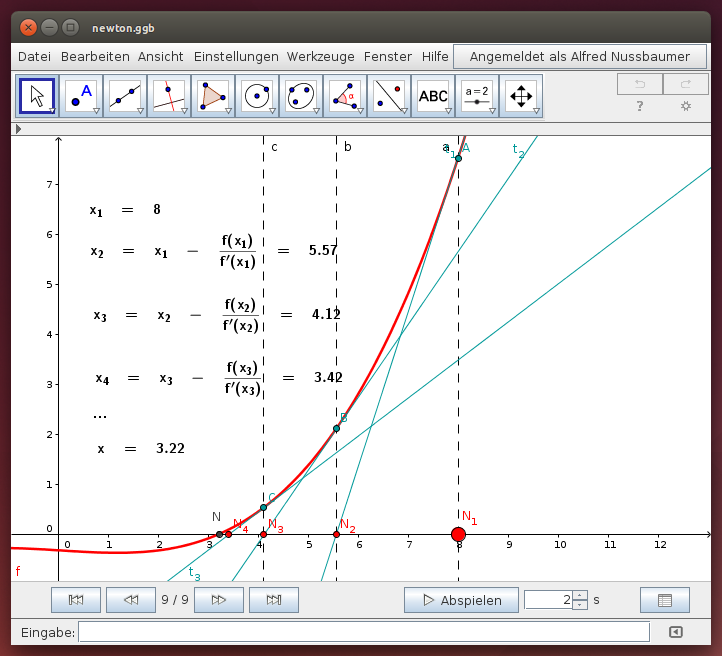
Führe das folgende GeoGebra-Beispiel schrittweise aus und beobachte, wie die vom Punkt ausgehend Punkte auf der Funktion gesucht werden, die immer näher zur gesuchten Nullstelle liegen. Starte die Konstruktion vom ersten Konstruktionsschritt aus:

Download der GeoGebra-Datei

• Begründe, warum die Tangenten „in Richtung der gesuchten Nullstelle“ weisen! Wann scheitert dieses Verfahren?
• Rechne die angegebene Iterationsformel für , , … nach!
• Verschiebe den Punkt N1 und beobachte die Lage der Tangenten! Schätze ab, nach wie vielen Iterationsschritten die gesuchte Nullstelle hinreichend genau bestimmt wurde!
• Vergleiche mit dem Bisektionsverfahren!
• Vergleiche mit der Regula Falsi!

zurück zu Alternative Lösungswege | Gleichungen und Ungleichungen | Polynomfunktionen | Nullstellen