Inhaltsverzeichnis
Polarkurven
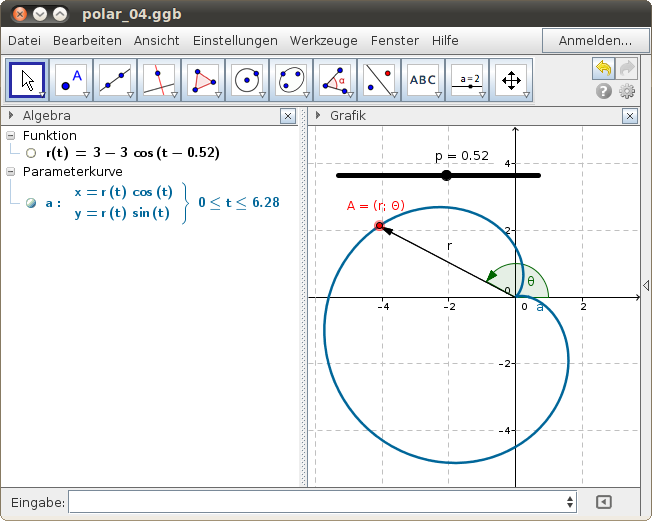
Für eine Reihe von Kurven ist die Polardarstellung günstig. Wir legen dabei den Radius r der Kurve als Funktion des Polarwinkels θ fest: r(θ).
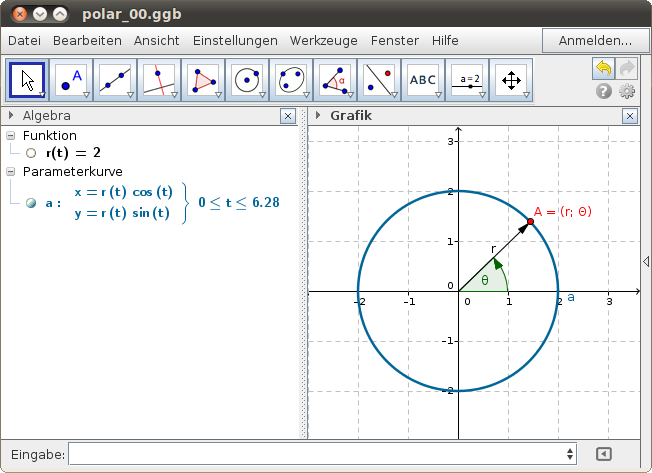
Beispiel: Polarkoordinaten beim Mittelpunktskreis
Der Kreis mit Radius 2 wird als Polarkurve definiert:
Hinweise:
- Im obigen Beispiel verwenden wir statt des Symboles θ einfach die Variable t.
- Für die Ausgabe als parametrisierte Kurve verwenden wir den GeoGebra-Befehl
Kurve(<Ausdruck in x>,<Ausdruck in y>,<Parameter>,<Startwert>,<Endwert>). Dazu wandeln wir die Polarkoordinaten ins rechtwinklige Koordinatensystem um:,
.
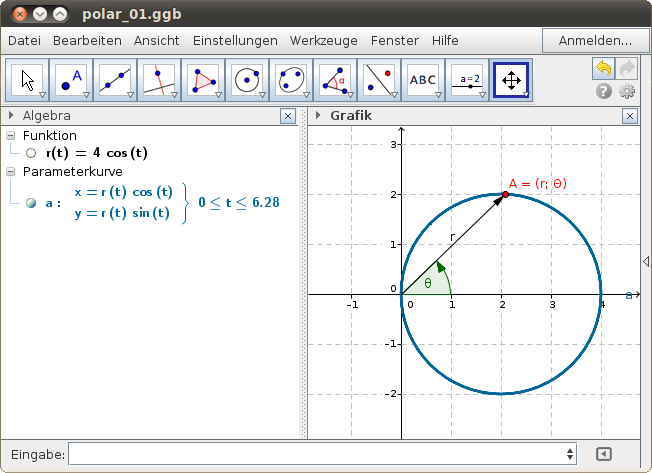
Beispiel: Kreis
Die Polarkurve legt einen Kreis mit Mittelpunkt M(2|0) und Radius 2 fest:
Wir rechnen nach:
daher: , M(2|0); r = 2
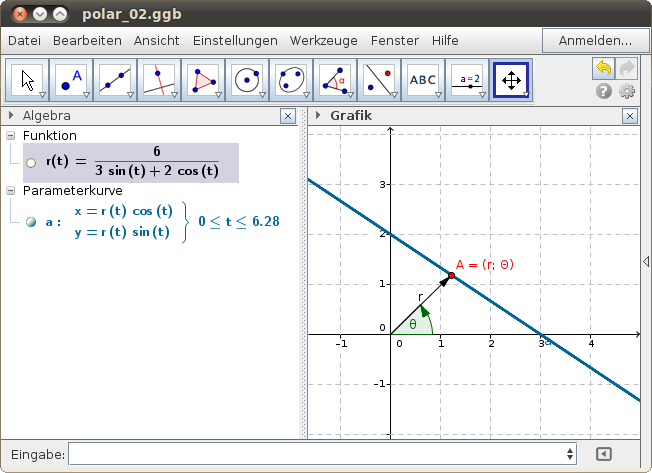
Beispiel: Gerade
Die Polarkurve legt eine Gerade fest:
Wir rechnen nach:
| Multiplikation mit dem Nenner liefert:
, und in Abschnittsform:
(vergleiche die Spurpunkte!)
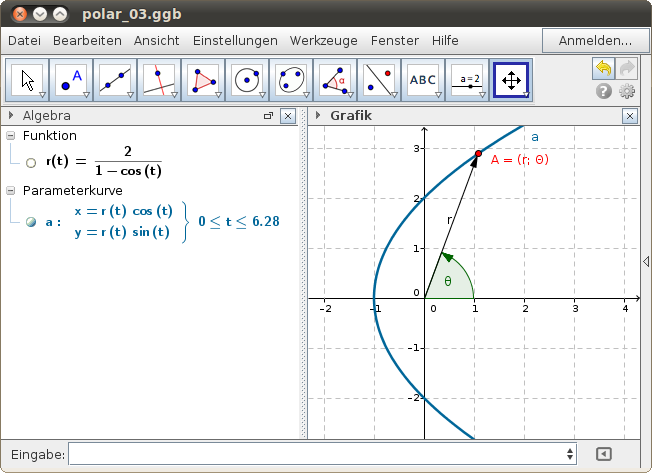
Beispiel: Parabel
Beispiel: Kardioide (Herzkurve)
Aufgaben:
- Stelle Spiralen als Polarkurven dar!
- Stelle Rosettenkurven als Polarkurven dar!
- Recherchiere weitere (parametrisierte) Kurven und bestimme ihre Polardarstellung!
- Vergleiche mit Lemniskaten!
Zurück zu parametrisierte Kurven